A Memory-Based Model of Syntactic Analysis: Data-Oriented Parsing


Remko Scha, Rens Bod and Khalil Sima'an

Institute for Logic, Language and Computation
University of Amsterdam
Spuistraat 134
1012 VB Amsterdam, The Netherlands

Abstract

This paper presents a memory-based model of human syntactic processing: Data-Oriented Parsing. After a brief introduction (section 1), it argues that any account of disambiguation and many other performance phenomena inevitably has an important memory-based component (section 2). It discusses the limitations of probabilistically enhanced competence-grammars, and argues for a more principled memory-based approach (section 3). In sections 4 and 5, one particular memory-based model is described in some detail: a simple instantiation of the "Data-Oriented Parsing" approach ("DOP1"). Section 6 reports on experimentally established properties of this model, and section 7 compares it with other memory-based techniques. Section 8 concludes and points to future work.

1. Introduction

Could it be the case that all of human language cognition takes place by means of similarity- and analogy-based processes which operate on a store of concrete past experiences? For those of us who are tempted to give a positive answer to this question, one of the most important challenges consists in describing the processes that deal with syntactic structure.

A person who knows a language can understand and produce a virtually endless variety of new and unforeseen utterances. To describe precisely how people actually do this, is clearly beyond the scope of linguistic theory; some kind of abstraction is necessary. Modern linguistics has therefore focussed its attention on the infinite repertoire of possible sentences (and their structures and interpretations) that a person's conception of a language in principle allows: the person's linguistic "competence".

In its effort to understand the nature of this "knowledge of language", linguistic theory uses the artificial languages of logic and mathematics as its paradigm sources of inspiration. Linguistic research proceeds on the assumption that a language is a well-defined formal code -- that to know a language is to know a non-redundant, consistent set of rules (a "competence grammar"), which establishes unequivocally which word sequences belong to the language, and what their pronunciations, syntactic analyses and semantic interpretations are.

Language-processing algorithms which are built for practical applications, or which are intended as cognitive models, must address some of the problems that linguistic competence grammars abstract away from. They cannot just produce the set of all possible analyses of an input utterance: in the case of ambiguity, they should pick the most plausible analysis; if the input is uncertain (as in the case of speech recognition) they should pick the most plausible candidate; if the input is corrupted (by typos or spelling-mistakes) they should make the most plausible correction.

A competence-grammar which gives a plausible characterization of the set of possible sentences of a language does no more (and no less) than provide a rather broad framework within which many different models of an individual's language processing capabilities ("performance models") may be specified. To investigate what a performance model of human language processing should look like, we do not have to start from scratch. We may, for instance, look at the ideas of previous generations of linguists and psychologists, even though these ideas did not yet get articulated as mathematical theories or computational models. If we do that, we find one very common idea: that language users produce and understand new utterances by constructing analogies with previously experienced ones. Noam Chomsky has noted, for instance, that this view was held by Bloomfield, Hockett, Jespersen, Paul, Saussure, and "many others" (Chomsky 1966, p. 12).

This intuitively appealing idea may be summarized as memory-based language-processing (if we want to emphasize that it involves accessing representations of concrete past language experiences), or as analogy-based language-processing (if we want to draw attention to the nature of the process that is applied to these representations). The project of embodying it in a formally articulated model seems a worthwhile challenge. In the next few sections of this paper we will discuss empirical reasons for actually undertaking such a project, and we will report on our first steps in that direction.

The next section therefore discusses in some detail one particular reason to be interested in memory-based models: the problem of ambiguity resolution. Section 3 will then start to address the technical challenge of designing a mathematical and computational system which complies with our intuitions about the memory-based nature of language-processing, while at the same time doing justice to some insights about syntactic structure which have emerged from the Chomskyan tradition.

2. Disambiguation and statistics

As soon as a formal grammar characterizes a non-trivial part of a natural language, it assigns an unmanageably large number of different analyses to almost every input string. This is problematic, because most of these analyses are not perceived as plausible by a human language user, although there is no conceivable clear-cut reason for a theory of syntax or semantics to label them as deviant (cf. Church & Patil, 1983; MacDonald et al., 1994; Martin et al., 1983.). Often, it is only a matter of relative implausibility. A certain interpretation may seem completely absurd to a human language user, just because another interpretation is much more plausible.

The disambiguation problem gets worse if the input is uncertain, and the system must explore alternative guesses about that. In spoken language understanding systems we encounter a very dramatic instance of this phenomenon. The speech recognition component of such a system usually generates many different guesses as to what the input word sequence might be, but it does not have enough information to choose between them. Just filtering out the 'ungrammatical' candidates is of relatively little help in this situation. The competence grammar of a language, being a characterization of the set of possible sentences and their structures, is clearly not intended to account for the disambiguation behavior of language users. Psycholinguistics and language technology, however, must account for such behavior; they must do this by embedding linguistic competence grammars in a proper theory of language performance.

There are many different criteria that play a role in human disambiguation behavior. First of all we should note that syntactic disambiguation is to some extent a side-effect of semantic disambiguation. People prefer plausible interpretations to implausible ones -- where the plausibility of an interpretation is assessed with respect to the specific semantic/pragmatic context at hand, taking into account conventional world knowledge (which determines what beliefs and desires we tend to attribute to others), social conventions (which determine what beliefs and desires tend to get verbally expressed), and linguistic conventions (which determine how they tend to get verbalized).

If we bracket out the influence of semantics and context, we notice another important factor that influences human disambiguation behavior: the frequency of occurrence of lexical items and syntactic structures. It has been established that (1) people register frequencies and frequency-differences (e.g. Hasher & Chromiak, 1977; Kausler & Puckett, 1980; Pearlmutter & MacDonald, 1992), (2) analyses that a person has experienced before are preferred to analyses that must be newly constructed (e.g. Hasher & Zacks, 1984; Jacoby & Brooks, 1984; Fenk-Oczlon, 1989), and (3) this preference is influenced by the frequency of occurrence of analyses: more frequent analyses are preferred to less frequent ones (e.g. Fenk-Oczlon, 1989; Mitchell et al., 1992; Juliano & Tanenhaus, 1993).

These findings are not surprising -- they are predicted by general information-theoretical considerations. A system confronted with an ambiguous signal may optimize its behavior by taking into account which interpretations are more likely to be correct than others -- and past occurrence frequencies may be the most reliable indicator for these likelihoods.

3. From probabilistic competence-grammars to data-oriented parsing

In the previous section we saw that the human language processing system seems to estimate the most probable analysis of a new input sentence, on the basis of successful analyses of previously encountered ones. But how is this done? What probabilistic information does the system derive from its past language experiences? The set of sentences that a language allows may best be viewed as infinitely large, and probabilistic information is used to compare alternative analyses of sentences never encountered before. A finite set of probabilities of units and combination operations must therefore be used to characterize an infinite set of probabilities of sentence-analyses.

This problem can only be solved if a more basic, non-probabilistic one is solved first: we need a characterization of the complete set of possible sentence-analyses of the language. As we saw before, that is exactly what the competence-grammars of theoretical syntax try to provide. Most probabilistic disambiguation models therefore build directly on that work: they characterize the probabilities of sentence-analyses by means of a "stochastic grammar", constructed out of a competence grammar by augmenting the rules with application probabilities derived from a corpus. Different syntactic frameworks have been extended in this way. Examples are Stochastic Context-Free Grammar (Suppes, 1970; Sampson, 1986; Black et al., 1992), Stochastic Lexicalized Tree-Adjoining Grammar (Resnik, 1992; Schabes, 1992), Stochastic Unification-Based Grammar (Briscoe & Carroll, 1993) and Stochastic Head-Driven Phrase Structure Grammar (Brew, 1995).

A statistically enhanced competence grammar of this sort defines all sentences of a language and all analyses of these sentences. It also assigns probabilities to each of these sentences and each of these analyses. It therefore makes definite predictions about an important class of performance phenomena: the preferences that people display when they must choose between different sentences (in language production and speech recognition), or between alternative analyses of sentences (in disambiguation).

The accuracy of these predictions, however, is necessarily limited. Stochastic grammars assume that the statistically significant language units coincide exactly with the lexical items and syntactic rules employed by the competence grammar. The most obvious case of frequency-based bias in human disambiguation behavior therefore falls outside their scope: the tendency to assign previously seen interpretations rather than innovative ones to platitudes and conventional phrases. Platitudes and conventional phrases demonstrate that syntactic constructions of arbitrary size and complexity may be statistically important, also if they are completely redundant from the point of view of a competence grammar.

Stochastic grammars which define their probabilities on minimal syntactic units thus have intrinsic limitations as to the kind of statistical distributions they can describe. In particular, they cannot account for the statistical biases which are created by frequently occurring complex structures. (For a more detailed discussion regarding some specific formalisms, see Bod (1995, Ch. 3).) The obvious way to remedy this, is to allow redundancy: to specify statistically significant complex structures as part of a "phrasal lexicon", even though the grammar could already generate these structures in a compositional way. To be able to do that, we need a grammar formalism which builds up a sentence structure out of explicitly specified component structures: a "Tree Grammar" (cf. Fu 1982). The simplest kind of Tree Grammar that might fit our needs is the formalism known as Tree Substitution Grammar (TSG).

A Tree Substitution Grammar describes a language by specifying a set of arbitrarily complex "elementary trees". The internal nodes of these trees are labelled by non-terminal symbols, the leaf nodes by terminals or non-terminals. Sentences are generated by a "tree rewrite process": if a tree has a leaf node with a non-terminal label, substitute on that node an elementary tree with that root label; repeat until all leaf nodes are terminals.

Tree Substitution Grammars can be arbitrarily redundant: there is no formal reason to disallow elementary trees which can also be generated by combining other elementary trees. Because of this property, a probabilistically enhanced TSG could model in a rather direct way how frequently occurring phrases and structures influence a language user's preferences and expectations: we could design a very redundant TSG, containing elementary trees for all statistically relevant phrases, and then assign the proper probabilities to all these elementary trees.

If we want to explore the possibilities of such Stochastic Tree Substitution Grammars (STSG's), the obvious next question is: what are the statistically relevant phrases? Suppose we have a corpus of utterances sampled from the population of expected inputs, and annotated with labelled constituent trees representing the contextually correct analyses of the utterances. Which subtrees should we now extract from this corpus to serve as elementary trees in our STSG?

There may very well be constraints on the form of cognitively relevant subtrees, but currently we do not know what they are. Note that if we only use subtrees of depth 1, the TSG is non-redundant: it would be equivalent to a CFG. If we introduce redundancy by adding larger subtrees, we can bias the analysis of previously experienced phrases and patterns in the direction of their previously experienced structures. We certainly want to include the structures of complete constituents and sentences for this purpose, but we may also want to include many partially lexicalized syntactic patterns.

Are there statistical constraints on the elementary trees that we want to consider? Should we only employ the most frequently occurring ones? That is not clear either. Psychological experiments have confirmed that the interpretation of ambiguous input is influenced by the frequency of occurrence of various interpretations in one's past experience . Apparently, the individual occurrences of these interpretations had a cumulative effect on the cognitive system. This implies that, at the time of a new occurrence, there is a memory of the previous occurrences. And in particular, that at the time of the second occurrence, there is a memory of the first. Frequency effects can only build up over time on the basis of memories of unique occurrences. The simplest way to allow this to happen is to store everything.

We thus arrive at a memory-based language processing model, which employs a corpus of annotated utterances as a representation of a person's past language experience, and analyses new input by means of an STSG which uses as its elementary trees all subtrees that can be extracted from the corpus, or a large subset of them. This approach has been called Data-Oriented Parsing (DOP). As we just summarized it, this model is crude and underspecified, of course. To build working sytems based on this idea, we must be more specific about subtree selection, probability calculations, parsing algorithms, and disambiguation criteria. These issues will be considered in the next few sections of this paper.

But before we do that, we should zoom out a little bit and emphasize that we do not expect that a simple STSG model as just sketched will be able to account for all linguistic and psycholinguistic phenomena that we may be interested in. We employ Stochastic Tree Substitution Grammar because it is a very simple kind of probabilistic grammar which allows us nevertheless to take into account the probabilities of arbitrarily complex subtrees. We do not believe that a corpus of contextless utterances with labelled phrase structure trees is an adequate model of someone's language experience, nor that syntactic processing is necessarily limited to subtree-composition. To build more adequate models, the corpus annotations will have to be enriched considerably, and more complex processes will have to be allowed in extracting data from the corpus as well as in analysing the input.

The general approach proposed here should thus be distinguished from the specific instantiations discussed in this paper. We can in fact articulate the overall idea fairly explicitly by indicating what is involved in specifying a particular technical instantiation (cf. Bod, 1995). To describe a specific "data-oriented processing" model, four components must be defined:

1. a formalism for representating utterance-analyses,
2. an extraction function which specifies which fragments or abstractions of the utterance- analyses may be used as units in constructing an analysis of a new utterance,
3. the combination operations that may be used in putting together new utterances out of fragments or abstractions,
4. a probability model which specifies how the probability of an analysis of a new utterance is computed on the basis of the occurrence-frequencies of the fragments or abstractions in the corpus.

Construed in this way, the data-oriented processing framework allows for a wide range of different instantiations. It then boils down to the hypothesis that human language processing is a probabilistic process that operates on a corpus of representations of past language experiences -- leaving open how the utterance-analyses in the corpus are represented, what sub-structures or other abstractions of these utterance-analyses play a role in processing new input, and what the details of the probabilistic calculations are.

Current DOP models are typically concerned with syntactic disambiguation, and employ readily available corpora which consist of contextless sentences with syntactic annotations. In such corpora, sentences are annotated with their surface phrase structures as perceived by a human annotator. Constituents are labeled with syntactic category symbols: a human annotator has designated each constituent as belonging to one of a finite number of mutually exclusive classes which are considered as potentially inter-substitutable.

Corpus-annotation necessarily occurs against the background of an annotation convention of some sort. Formally, this annotation convention constitutes a grammar, and in fact, it may be considered as a competence grammar in the Chomskyan sense: it defines the set of syntactic structures that is possible. We do not presuppose, however, that the set of possible sentences, as defined by the representational formalism employed, coincides with the set of sentences that a person will judge to be grammatical. The competence grammar as we construe it, must be allowed to overgenerate: as long as it generates a superset of the grammatical sentences and their structures, a properly designed probabilistic disambiguation mechanism may be able to distinguish grammatical sentences and grammatical structures from their ungrammatical or less grammatical alternatives. An annotated corpus can thus be viewed as a stochastic grammar which defines a subset of the sentences and structures allowed by the annotation scheme, and which assigns empirically motivated probabilities to each of these sentences and structures.

The current paper thus explores the properties of some varieties of a language-processing model which embodies this approach in a stark and simple way. The model demonstrates that memory-based language-processing is possible in principle. For certain applications it performs better already than some probabilistically enhanced competence-grammars, but its main goal is to serve as a starting point for the development of further refinements, modifications and generalizations.

4. A Simple Data-Oriented Parsing Model: DOP1

We will now look in some detail at one simple DOP model, which is known as DOP1 (Bod 1992, 1993a, 1995). Consider a corpus consisting of only two trees, labeled with conventional syntactic categories:

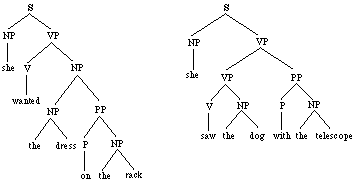
Figure 1. Imaginary corpus of two trees.

Various subtrees can be extracted from the trees in such a corpus. The subtrees we consider are: (1) the trees of complete constituents (including the corpus trees themselves, but excluding individual terminal nodes); and (2) all trees that can be constructed out of these constituent trees by deletiing proper subconstituent trees and replacing them by their root nodes.

The subtree-set extracted from a corpus defines a Stochastic Tree Substitution Grammar. The stochastic sentence generation process of DOP1 employs only one operation for combining subtrees, called "composition", indicated as o. The composition-operation identifies the leftmost nonterminal leaf node of one tree with the root node of a second tree, i.e., the second tree is substituted on the leftmost nonterminal leaf node of the first tree. Starting out with the "corpus" of Figure 1 above, for instance, the sentence "She saw the dress with the telescope", may be generated by repeated application of the composition operator to corpus subtrees in the following way:

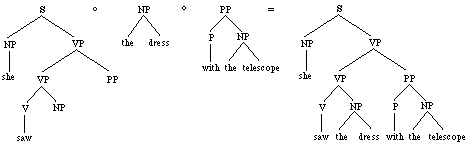
Figure 2. Derivation and parse for "She saw the dress with the telescope"

Several other derivations, involving different subtrees, may of course yield the same parse tree; for instance:

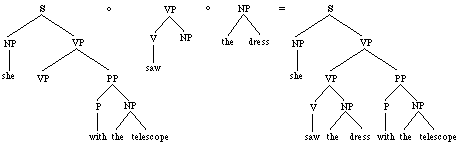
or

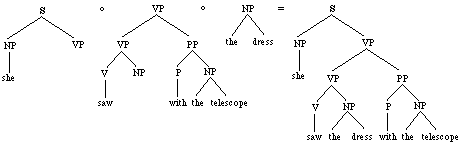
Figures 3/4. Two other derivations of the same parse for
"She saw the dress with the telescope".

Note also that, given this example corpus, the sentence we considered is ambiguous; by combining other subtrees, a different parse may be derived, which is analogous to the first rather than the second corpus sentence.

DOP1 computes the probability of substituting a subtree t on a specific node as the probability of selecting t among all corpus-subtrees that could be substituted on that node. This probability is equal to the number of occurrences of t, |t|, divided by the total number of occurrences of subtrees t' with the same root label as t. Let r (t) return the root label of t. Then we may write:

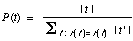
Since each node substitution is independent of previous substitutions, the probability of a derivation D = t1 o . . . o tn is computed by the product of the probabilities of the subtrees ti involved in it:

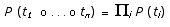
The probability of a parse tree is the probability that it is generated by any of its derivations. The probability of a parse tree T is thus computed as the sum of the probabilities of its distinct derivations D:

This probability may be viewed as a measure for the average similarity between a sentence analysis and the analyses of the corpus utterances: it correlates with the number of corpus trees that share subtrees with the sentence analysis, and also with the size of these shared fragments. Whether this measure constitutes an optimal way of weighing frequency and size against each other, is a matter of empirical investigation.

5. Computational Aspects of DOP1

We now consider the problems of parsing and disambiguation with DOP1. The algorithms we discuss do not exploit the particular properties of Data-Oriented Parsing; they work with any Stochastic Tree-Substitution Grammar.

5.1 Parsing

The algorithm that creates a parse forest for an input sentence is derived from algorithms that exist for Context-Free Grammars, which parse an input sentence of n words in polynomial (usually cubic) time. These parsers use a chart or well-formed substring table. They take as input a set of context-free rewrite rules and a sentence and produce as output a chart of labeled phrases. A labeled phrase is a sequence of words labeled with a category symbol which denotes the syntactic category of that phrase. A chart-like parse forest can be obtained by including pointers from a category to the other categories which caused it to be placed in the chart. Algorithms that accomplish this can be found in e.g. Kay (1980), Winograd (1983), Jelinek et al. (1990).

The chart parsing approach can be applied to parsing with Stochastic Tree-Substitution Grammars if we note that every elementary tree t of the STSG can be viewed as a context-free rewrite rule: root(t) —> yield(t) (cf. Bod 1992). In order to obtain a chart-like forest for a sentence parsed with an STSG, we label the phrases not only with their syntactic categories but with their full elementary trees. Note that in a chart-like forest generated by an STSG, different derivations that generate identical trees do not collapse. We will therefore talk about a derivation forest generated by an STSG (cf. Sima'an et al. 1994).

We now show what such a derivation forest may look like. Assume an example STSG which has the trees in Figure 5 as its elementary trees. A chart parser analysing the input string abcd on the basis of this STSG, will then create the derivation forest illustrated in Figure 6. The visual representation is based on Kay (1980): every entry (i,j) in the chart is indicated by an edge and spans the words between the i-th and the j-th position of a sentence. Every edge is labeled with linked elementary trees that constitute subderivations of the underlying subsentence. (The probabilities of the elementary trees, needed in the disambiguation phase, have been left out.)

 

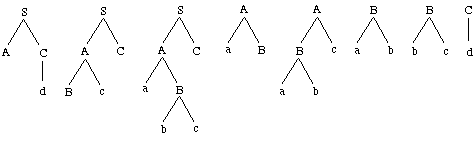
Figure 5. Elementary trees of an example STSG.

 

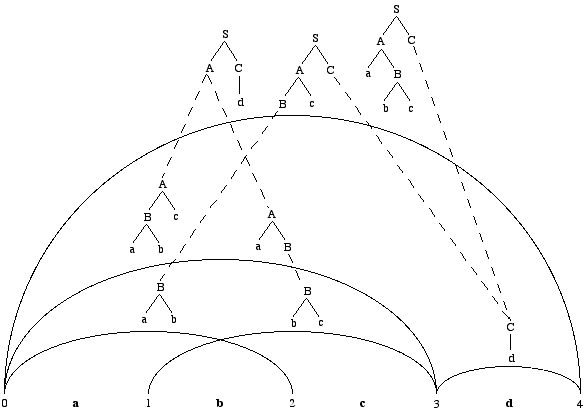
Figure 6. Derivation forest for the string abcd.

Note that some of the derivations in the forest generate the same tree. By exhaustively unpacking the forest, four different derivations generating two different trees are obtained. Both trees are generated twice, by different derivations (with possibly different probabilities).

5.2 Disambiguation

The derivation forest defines all derivations (and thereby all parses) of the input sentence. Disambiguation now consists in choosing the most likely parse within this set of possibilities. The stochastic model of DOP1 as described above specifies a definite disambiguation criterion that may be used for this purpose: it assigns a probability to every parse tree by accumulating the probabilities of all its different derivations; these probabilities define the most probable parse (MPP) of a sentence.

We may expect that the most probable derivation (MPD) of a sentence, which is simpler to compute, often yields a parse which is identical to the most probable parse. If this is indeed the case, the MPD may be used to estimate the MPP (cf. Bod 1993a, Sima'an 1995). We now discuss first the most probable derivation and then the most probable parse.

5.2.1 The most probable derivation

A cubic time algorithm for computing the most probable derivation of a sentence can be designed on the basis of the well-known Viterbi algorithm (Viterbi 1967; Jelinek et al. 1990; Sima'an 1995). The basic idea of Viterbi is the elimination of low probability subderivations in a bottom-up fashion. Two different subderivations of the same part of the sentence whose resulting subparses have the same root can both be developed (if at all) to derivations of the whole sentence in the same ways. Therefore, if one of these two subderivations has a lower probability, it can be eliminated.

The computation of the most probable derivation from a chart generated by an STSG can be accomplished by selecting at every chart-entry the most probable subderivation for each root-node, while the other subderivations for that root-node are eliminated. We will not give the full algorithm here, but its structure can be gleaned from the algorithm which computes the probability of the most derivation:

Algorithm 1: Computing the probability of the most probable derivation

Given an STSG, let S denote its start non-terminal, R denote its set of elementary trees, and P denote its probability function over the elementary trees. Let us assume for the moment that the elementary trees of the STSG are in Chomsky Normal Form (CNF), i.e. every elementary tree has either two frontier nodes both labeled by non-terminals, or one frontier node labeled by a terminal. An elementary tree t that has root label A and a sequence of ordered frontier labels H is represented by A—>t H. Let the triple <A, i, j> denote the fact that non-terminal A is in chart entry (i, j) after parsing the input string W1,...,Wn; this implies that the STSG can derive the substring Wi+1,...,Wj, starting with an elementary tree that has root label A. The probability of the MPD of string W1,...,Wn, represented as PPMPD, is computed recursively as follows:

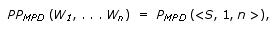
where

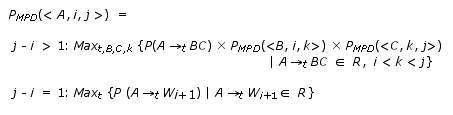
Obviously, if we drop the CNF assumption, we may apply exactly the same strategy. And by introducing some bookkeeping to keep track of the subderivations which yield the highest probabilities at each step, we get an algorithm which actually computes the most probable derivation. (For some more detail, see Sima'an et al. 1994.)

5.2.2 The most probable parse

The most probable parse tree of a sentence cannot be computed in deterministic polynomial time: Sima'an (1996b) proved that for STSG's the problem of computing the most probable parse is NP-hard. This does not mean, however, that every disambiguation algorithm based on this notion is necessarily intractable. We will now investigate to what extent tractability may be achieved if we forsake analytical probability calculations, and are satisfied with estimations instead.

Because the derivation forest specifies a statistical ensemble of derivations, we may employ the Monte Carlo method (Hammersley & Handscomb 1964) for this purpose: we can estimate parse tree probabilities by sampling a suitable number of derivations from this ensemble, and observing which parse tree results most frequently from these derivations.

We have seen that a best-first search, as accomplished by Viterbi, can be used for computing the most probable derivation from the derivation forest. In an analogous way, we may conduct a random-first search, which selects a random derivation from the derivation forest by making, for each node at each chart-entry, a random choice between the different alternative subtrees on the basis of their respective substitution probabilities. By iteratively generating several random derivations we can estimate the most probable parse as the parse which results most often from these derivations. (The probability of a parse is the probability that any of its derivations occurs.) According to the Law of Large Numbers, the most frequently generated parse converges to the most probable parse as we increase the number of derivations that we sample.

This strategy is exemplified by the following algorithm (Bod 1993b, 95):

Algorithm 2: Sampling a random derivation

Given a derivation forest of a sentence of n words, consisting of labeled entries (i,j) that span the words between the ith and the jth position of the sentence. Every entry is labeled with elementary trees, each with its probability and, for every non-terminal leaf node, a pointer to the relevant sub-entry. (Cf. Figure 6 in Section 5.1 above.) Sampling a derivation from such a chart consists of choosing at random one of the elementary trees for every root-node at every labeled entry (e.g. bottom-up, breadth-first):

for length := 1 to n do
    for start := 0 to n - length do
         for each root node X in chart-entry (start, start + length) do
                select at random a tree from the distribution of elementary trees with root node X;
                eliminate the other elementary trees with root node X from this chart-entry

The resulting randomly pruned derivation forest trivially defines one "random derivation" for the whole sentence: take the elementary tree of chart-entry (0, n) and recursively substitute the elementary subtrees of the relevant sub-entries on non-terminal leaf nodes.

The parse tree that results from this derivation constitutes a first guess for the most probable parse. A more reliable guess can be computed by sampling a larger number of random derivations, and selecting the parse which results most often from these derivations. How large a sample set should be chosen?

Let us first consider the probability of error: the probability that the parse that is most frequently generated by the sampled derivations, is in fact not equal to the most probable parse. An upper bound for this probability is given by
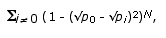where the different values of i are indices corresponding to the different parses, 0 is the index of the most probable parse, pi is the probability of parse i; and N is the number of derivations that was sampled (cf. Hammersley & Handscomb 1964).

This upper bound on the probability of error becomes small if we increase N, but if there is an i with pi close to p0 (i.e., if there are different parses in the top of the sampling distribution that are almost equally likely), we must make N very large to achieve this effect. If there is no unique most probable parse, the sampling process will of course not converge on one outcome. In that case, we are interested in all of the parses that outrank all the other ones. But also when the probabilities of the most likely parses are very close together without being exactly equal, we may be interested not in the most probable parse, but in the set of all these almost equally highly probable parses. This reflects the situation in which there is an ambiguity which cannot be resolved by probabilistic syntactic considerations.

We conclude, therefore, that the task of a syntactic disambiguation component is the calculation of the probability distribution of the various possible parses, and only in the case of a forced choice experiment we choose the parse with the highest probability from this distribution (cf. Bod & Scha 1997). When we estimate this probability distribution by statistical methods, we must establish the reliability of this estimate. This reliability is characterized by the probability of significant errors in the estimates of the probabilities of the various parses.

If a parse has probability pi, and we try to estimate the probability of this parse by its frequency in a sequence of N independent samples, the variance in the estimated probability is pi(1 - pi)/N. Since 0 < pi ² 1, the variance is always smaller than or equal to 1/(4N). Thus, the standard error s, which is the square root of the variance, is always smaller than or equal to 1/(2 sqrt(N)). This allows us to calculate a lower bound for N given an upper bound for s, by N ³ 1/(4 square(s)). For instance, we obtain a standard error s ² 0.05 if N ³ 100.

We thus arrive at the following algorithm:

Algorithm 3: Estimating the parse probabilities

Given a derivation forest of a sentence and a threshold sM for the standard error:

N := the smallest integer larger than 1/(4 square(sM))

repeat N times:

sample a random derivation from the derivation forest;
store the parse generated by this derivation;

for each parse i:

estimate the conditional probability given the sentence by pi := #(i) / N

In the case of a forced choice experiment we select the parse with the highest probability from this distribution. Rajman (1995) gives a correctness proof for Monte Carlo disambiguation; he shows that the probability of sampling a parse i from a derivation forest of a sentence w is equal to the conditional probability of i given w: P(i|w).

Note that this algorithm differs essentially from the disambiguation algorithm given in Bod (1995), which increases the sample size until the probability of error of the MPP estimation has become sufficiently small. That algorithm takes exponential time in the worst case, though this was overlooked in the complexity discussion in Bod (1995). (This was brought to our attention in personal conversation by Johnson (1995) and in writing by Goodman (1996, 1998).)

The present algorithm (from Bod & Scha 1996, 1997) therefore focuses on estimating the distribution of the parse probabilities; it assumes a value for the maximally allowed standard error (e.g. 0.05), and samples a number of derivations which is guaranteed to achieve this; this number is quadratic in the chosen standard error. Only in the case of a forced choice experiment, the most frequently occurring parse is selected from the sample distribution.

5.2.3 Optimizations

In the past few years, several optimizations have been proposed for disambiguating with STSG. Sima'an (1995, 1996a) gives an optimization for computing the most probable derivation which starts out by using only the CFG-backbone of an STSG; subsequently, the constraints imposed by the STSG are employed to further restrict the parse space and to select the most probable derivation. This optimization achieves linear time complexity in STSG size without risking an impractical increase of memory-use. Bod (1993b, 1995) proposes to use only a small random subset of the corpus subtrees (5%) so as to reduce the search space for computing the most probable parse. Sekine and Grishman (1995) use only subtrees rooted with S or NP categories, but their method suffers considerably from undergeneration. Goodman (1996) proposes a different polynomial time disambiguation strategy which computes the so-called "maximum constituents parse" of a sentence (i.e. the parse which maximizes the expected number of correct constituents) rather than the most probable parse or most probable derivation. However, Goodman also shows that the "maximum constituents parse" may return parse trees that cannot be produced by the subtrees of DOP1 (Goodman 1996: 147). Chappelier & Rajman (1998) and Goodman (1998) give some optimizations for selecting a random derivation from a derivation forest. For a more extensive discussion of these and some other optimization techniques see Bod (1998a) and Sima'an (1999).

6. Experimental Properties of DOP1

In this section, we establish some experimental properties of DOP1. We will do so by studying the impact of various fragment restrictions.

6.1 Experiments on the ATIS corpus

We first summarize a series of pilot experiments carried out by Bod (1998a) on a set of 750 sentence analyses from the Air Travel Information System (ATIS) corpus (Hemphill et al. 1990) that were annotated in the Penn Treebank (Marcus et al. 1993). [1] These experiments focussed on tests about the Most Probable Parse as defined by the original DOP1 probability model. [2] Their goal was not primarily to establish how well DOP1 would perform on this corpus, but to find out how the accuracies obtained by "undiluted" DOP1 compare with the results obtained by more restricted STSG-models which do not employ the complete set of corpus subtrees as their elementary trees.

We use the blind testing method, dividing the 750 ATIS trees into a 90% training set of 675 trees and a 10% test set of 75 trees. The division was random except for one constraint: that all words in the test set actually occurred in the training set. [3] The 675 training set trees were converted into fragments (i.e. subtrees) and were enriched with their corpus probabilities. The 75 sentences from the test set served as input sentences that were parsed with the subtrees from the training set and disambiguated by means of the algorithms described in the previous section. The most probable parses were estimated from probability distributions of 100 sampled derivations. We use the notion of parse accuracy as our accuracy metric, defined as the percentage of the most probable parses that are identical to the corresponding test set parses.

Because the MPP estimation is a fairly costly algorithm, we have not yet been able to repeat all our experiments for different training-set/test-set splits, to obtain average results with standard deviations. We made one exception, however. We will very often be comparing the results of an experiment with the results obtained when employing all corpus-subtrees as elementary trees; therefore, it was important to establish at least that the parse accuracy obtained in this fashion (which was 85%) was not due to some unlikely random split.

On 10 random training/test set splits of the ATIS corpus we achieved an average parse accuracy of 84.2% with a standard deviation of 2.9%. Our 85% base line accuracy lies thus solidly within the range of values predicted by the more extentensive experiment.

The impact of overlapping fragments: MPP vs. MPD

The stochastic model of DOP1 can generate the same parse in many different ways; the probability of a parse must therefore be computed as the sum of the probabilities of all its derivations. We have seen, however, that the computation of the Most Probable Parse according to this model has an unattractive complexity, whereas the Most Probable Derivation is much easier to compute. We may therefore wonder how often the parse generated by the Most Probable Derivation is in fact the correct one: perhaps this method constitutes a good approximation of the Most Probable Parse, and can achieve very similar parse accuracies. And we cannot exclude that it might yield even better accuracies, if it somehow compensates for bad properties of the stochastic model of DOP1. For instance, by summing up over probabilities of several derivations, the Most Probable Parse takes into account overlapping fragments, while the Most Probable Derivation does not. It is not a priori obvious whether we do or do not want this property.

We thus calculated the accuracies based on the analyses generated by the Most Probable Derivations of the test sentences. The parse accuracy obtained by the trees generated by the Most Probable Derivations was 69%, which is lower than the 85% base line parse accuracy obtained by the Most Probable Parse. We conclude that overlapping fragments play an important role in predicting the appropriate analysis of a sentence.

The impact of fragment size

Next, we tested the impact of the size of the fragments on the parse accuracy. Large fragments capture more lexical/syntactic dependencies than small ones. We investigated to what extent this actually leads to better predictions of the appropriate parse. We therefore performed experiments with versions of DOP1 where the fragment collection is restricted to subtrees with a certain maximum depth (where the depth of a tree is defined as the length of the longest path from the root to a leaf). For instance, restricting the maximum depth of the subtrees to 1 gives us fragments that cover exactly one level of constituent structure, which makes DOP1 equivalent to a stochastic context-free grammar (SCFG). For a maximal subtree depth of 2, we obtain fragments that also cover two levels of constituent structure, which capture some more lexical/syntactic dependencies, etc. The following table shows the results of these experiments, where the parse accuracy for each maximal depth is given for both the most probable parse and for the parse generated by the most probable derivation (the accuracies are rounded off to the nearest integer).

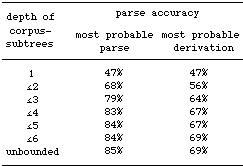
Table 1. Accuracy increases if larger corpus fragments are used

The table shows an increase in parse accuracy, for both the most probable parse and the most probable derivation, when enlarging the maximum depth of the subtrees. The table confirms that the most probable parse yields better accuracy than the most probable derivation, except for depth 1 where DOP1 is equivalent to an SCFG (and where every parse is generated by exactly one derivation). The highest parse accuracy reaches 85%.

The impact of fragment lexicalization

We now consider the impact of lexicalized fragments on the parse accuracy. By a lexicalized fragment we mean a fragment whose frontier contains one or more words. The more words a fragment contains, the more lexical (collocational) dependencies are taken into account. To test the impact of lexicalizationon the parse accuracy, we performed experiments with different versions of DOP1 where the fragment collection is restricted to subtrees whose frontiers contain a certain maximum number of words; the maximal subtree depth was kept constant at 6.

These experiments are particularly interesting since we can simulate lexicalized grammars in this way. Lexicalized grammars have become increasingly popular in computational linguistics (e.g. Schabes 1992; Srinivas & Joshi 1995; Collins 1996, 1997; Charniak 1997; Carroll & Weir 1997). However, all lexicalized grammars that we know of restrict the number of lexical items contained in a rule or elementary tree. It is a significant feature of the DOP approach that we can straightforwardly test the impact of the number of lexical items allowed.

The following table shows the results of our experiments, where the parse accuracy is given for both the most probable parse and the most probable derivation.

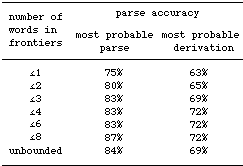
Table 2. Accuracy as a function of the maximum number of words in fragment frontiers.

The table shows an initial increase in parse accuracy, for both the most probable parse and the most probable derivation, when enlarging the amount of lexicalization that is allowed. For the most probable parse, the accuracy is stationary when the maximum is enlarged from 4 to 6 words, but it increases again if the maximum is enlarged to 8 words. For the most probable derivation, the parse accuracy reaches its maximum already at a lexicalization bound of 4 words. Note that the parse accuracy deteriorates if the lexicalization bound exceeds 8 words. Thus, there seems to be an optimal lexical maximum for the ATIS corpus. The table confirms that the most probable parse yields better accuracy than the most probable derivation, also for different lexicalization sizes.

The impact of fragment frequency

We may expect that highly frequent fragments contribute to a larger extent to the prediction of the appropriate parse than very infrequent fragments. But while small fragments can occur very often, most larger fragments typically occur once. Nevertheless, large fragments contain much lexical/structural context, and can parse a large piece of an input sentence at once. Thus, it is interesting to see what happens if we systematically remove low-frequency fragments. We performed an additional set of experiments by restricting the fragment collection to subtrees with a certain minimum number of occurrences, but without applying any other restrictions.

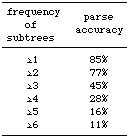
Table 3. Accuracy decreases if lower bound on fragment frequency increases
(for the most probable parse).

The results, presented in Table 3, indicate that low frequency fragments contribute significantly to the prediction of the appropriate analysis: the parse accuracy seriously deteriorates if low frequency fragments are discarded. This seems to contradict common wisdom that probabilities based on sparse data are not reliable. Since especially large fragments are once-occurring events, there seems to be a preference in DOP1 for an occurrence-based approach if enough context is provided: large fragments, even if they occur once, tend to contribute to the prediction of the appropriate parse, since they provide much contextual information. Although these fragments have very low probabilities, they tend to induce the most probable parse because fewer fragments are needed to construct a parse.

In Bod (1998a), the impact of some other fragment restrictions is studied. Among other things, it is shown there that the parse accuracy decreases if subtrees with only non-head words are eliminated.

6.2 Experiments on larger corpora: the SRI-ATIS corpus and the OVIS corpus

In the following experiments (summarized from Sima'an 1999) [4] we only employ the most probable derivation rather than the most probable parse. Since the most probable derivation can be computed more efficiently than the most probable parse (see section 5), it can be tested more extensively on larger corpora. The experiments were conducted on two domains: the Amsterdam OVIS tree-bank (Bonnema et al. 1997) and the SRI-ATIS tree-bank (Carter 1997). [5] It is worth noting that the SRI-ATIS tree-bank differs considerably from the Penn Treebank ATIS-corpus that was employed in the experiments reported in the preceding subsection.

In order to acquire workable and accurate DOP1 models from larger tree-banks, a set of heuristic criteria is used for selecting the fragments. Without these criteria, the number of subtrees would not be manageable. For example, in OVIS there are more than hunderd and fifty million subtrees. Even when the subtree depth is limited to e.g. depth five, the number of subtrees in the OVIS tree-bank remains more than five million. The subtree selection criteria are expressed as constraints on the form of the subtrees that are projected from a tree-bank into a DOP1 model. The constraints are expressed as upper-bounds on: the depth (d), the number of substitution-sites (n), the number of terminals (l) and the number of consecutive terminals (L) of the subtree. These constraints apply to all subtrees but the subtrees of depth 1, i.e. subtrees of depth 1 are not subject to these selection criteria. In the sequel we represent the four upper-bounds by the short notation ddnnllLL. For example, d4n2l7L3 denotes a DOP STSG obtained from a tree-bank such that every elementary tree has at most depth 4, and a frontier containing at most 2 substitution sites and 7 terminals; moreover, the length of any consecutive sequence of terminals on the frontier of that elementary tree is limited to 3 terminals. Since all projection parameters except for the upper-bound on the depth are usually a priori fixed, the DOP1 STSG obtained under a depth upper-bound that is equal to an integer i will be represented by the short notation DOP(i).

We used the following evaluation metrics: Recognized (percentage of recognized sentences), TLC (Tree-Language Coverage: the percentage of test set parses that is in the tree language of the DOP1 STSG), exact match (either syntactic/semantic or only syntactic), labeled bracketing recall and precision (as defined in Black et al. 1991, concerning either syntactic plus semantic or only syntactic annotation). Below we summarize the experimental results pertaining to some of the issues that are addressed in Sima'an (1999). Some of these issues are similar to those addressed by the experiments with the most probable parse on the small ATIS tree-bank in subsection 6.1, e.g. the impact of fragment size. Other issues are orthogonal and supplement the issues addressed in the experiments concerning the most probable parse.

Experiments on the SRI-ATIS corpus

In this section we report experiments on syntactically annotated utterances from the SRI International ATIS tree-bank. The utterances of the tree-bank originate from the ATIS domain (Hemphill et al. 1990). For the present experiments, we have access to 13335 utterances that are annotated syntactically (we refer to this tree-bank here as the SRI-ATIS corpus/tree-bank). The annotation scheme originates from the linguistic grammar that underlies the Core Language Engine (CLE) system in Alshawi (1992). The annotation process is described in Carter (1997). For the experiments summarized below, some of the training parameters were fixed: the DOP models were projected under the parameters n2l4L3, while the subtree depth bound was allowed to vary.

A training-set of 12335 trees and a test-set of 1000 trees were obtained by partitioning the SRI-ATIS tree-bank randomly. DOP1 models with various depth upper-bound values were trained on the training-set and tested on the test-set. It is noteworthy that the present experiments are extremely time-consuming: for upper-bound values larger than three, the models become huge and very slow, e.g. it takes more than 10 days for DOP(4) to parse and disambiguate the test-set (1000 sentences). This is despite of the subtree upper bounds n2l4L3, which limit the total size of the subtree-set to less than three hunderd thousand subtrees.

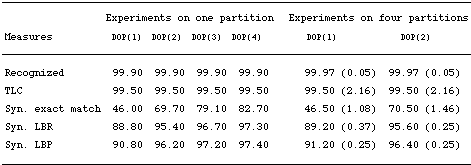
Table 4. The impact of subtree depth (SRI-ATIS)

Table 4 (left-hand side) shows the results for depth upper-bound values up to four. An interesting and suprising result is that the exact-match of DOP(1) on this larger and different ATIS tree-bank (46%) is very close to the result reported in the preceding subsection. This also holds for the DOP(4) model (here 82.70% exact-match vs. 84% on the Penn Treebank ATIS corpus). More striking is that the present experiments concern the most probable derivation while the experiments of the preceding section concern the most probable parse. In the preceding subsection, the exact-match of the most probable derivation did not exceed 69%, while in this case it is 82.70%. This might be explained by the fact that the availability of more data is more crucial for the accuracy of the most probable derivation than the most probable parse. This is certainly not due to a simpler tree-bank or domain since the annotations here are as deep as those in the Penn Treebank. In any case, it would be interesting to consider the exact match that the most probable pare achieves on this tree-bank. This, however, will remain an issue for future research because computing the most probable parse is still infeasible on such large tree-banks.

The issue of course here is still the impact of employing deeper subtrees. Clearly, as the results show, the difference between the DOP(1) (the SCFG) and any deeper DOP1 model is at least 23% (DOP(2)). This difference increases to 36.70% at DOP(4). To validate this difference, we ran experiments with a four-fold cross-validation experiment that confirms the magnitude of this difference. In the right-hand side of table 4 means and standard-deviations for two DOP1 models are reported. Four independent partitions into test (1000 trees each) and training sets (12335 trees each) were used here for training and testing these DOP1 models. These results show a mean difference of 24% exact-match between DOP(2) and DOP(1) (SCFG): a substantial accuracy improvement achieved by memory-based parsing using DOP1, above simply using the SCFG underlying the tree-bank (as for instance in Charniak 1996).

Experiments on the OVIS corpus

The Amsterdam OVIS ("Openbaar Vervoer Informatie Systeem") corpus contains 10000 syntactically and semantically annotated trees. For detailed information concerning the syntactic and semantic annotation scheme of the OVIS tree-bank we refer the reader to Bonnema et al. (1997). In acquiring DOP1 models the semantic and syntactic annotations are treated as one annotation in which the labels of the nodes in the trees are a juxtaposition of the syntactic and semantic labels. Although this results in many more non-terminal symbols (and thus also DOP model parameters), Bonnema (1996) shows that the resulting syntactic+semantic DOP models are better than the mere syntactic DOP1 models. Since the utterances in the OVIS tree-bank are answers to questions asked by a dialogue system, these utterances tend to be short. The average sentence length in OVIS is 3.43 words. However, the results reported in Sima'an (1999) concern only sentences that contain at least two words; the number of those sentences is 6797 and their average length is 4.57 words. All DOP1 models are projected under the subtree selection criterion n2l7L3, while the subtree depth upper bound was allowed to vary.

It is interesting here to observe the effect of varying subtree depth on the performance of the DOP1 models on a tree-bank from a different domain. To this end, in a set of experiments one random partition of the OVIS tree-bank into a test-set of 1000 trees and a training set of 9000 was used to test the effect of allowing the projection of deeper elementary trees in DOP STSGs. DOP STSGs were projected from the training set with upper-bounds on subtree depth equal to 1, 3, 4, and 5. Each of the four DOP models was run on the sentences of the test-set (1000 sentences). The resulting parse trees were then compared to the correct test set trees.

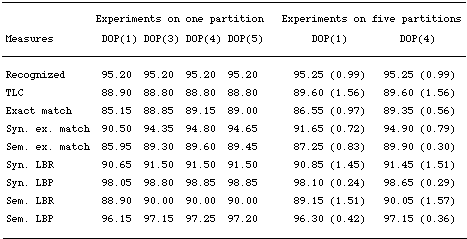
Table 5. The impact of subtree depth (OVIS)

The lefthand side of table 5 above shows the results of these DOP1 models. Note that the recognition power (Recognized) is not affected by the depth upper-bound in any of the DOP1 models. This is because all models allowed all subtrees of depth 1 to be elementary trees. As the results show, a slight accuracy degradation occurs when the subtree depth upper bound is increased from four to five. This has been confirmed separately by earlier experiments conducted on similar material (Bonnema et al. 1997). An explanation for this degradation might be that including larger subtrees implies many more subtrees and sparse-data effects. It is not clear, therefore, whether this finding contradicts the Memory-Based Learning doctrine that maintaining all cases in the case-base is more profitable. It might equally well be the case that this problem is specific for the DOP1 model and the way it assigns probabilities to subtrees.

Table 5 also shows the means and standard deviations (stds) of two DOP1 models on five independent partitions of the OVIS tree-bank into training set (9000 trees) and test set (1000 trees). For every partition, the DOP1 model was trained only on the training set and then tested on the test set. We observe here the means and standard deviation of the models DOP(1) (the SCFG underlying the tree-bank) and DOP(4). Clearly, the difference between DOP(4) and DOP(1) observed in the preceding set of experiments is supported here. However, the improvement of DOP(4) on the SCFG in exact match and the other accuracy measures, although significant, is disappointing: it is about 2.85% exact match and 3.35% syntactic exact match. The improvement itself is indeed in line with the observation that DOP1 improves on the SCFG underlying the tree-bank. This can be seen as an argument for MBL syntactic analysis as opposed to the traditional enrichment of "linguistic" grammars with probabilities.

We have thus seen that there is quite some evidence for our hypothesis that the structural units of language processing cannot limited to a minimal set of rules, but should be defined in terms of a large set of previously seen structures. It is interesting to note that similar results are obtained by other instantiations of memory-based language processing. For example, van den Bosch & Daelemans (1998) report that almost every criterion for removing instances from memory yields worse accuracy than keeping full memory of learning material (for the task of predicting English word pronunciation). Despite this interesting convergence of results, there is a significant difference between DOP and other memory-based approaches. We will go into this topic in the following section.

7. DOP: probabilistic recursive MBL

In this section we make explicit the relationship between the present Data Oriented Processing (DOP) framework and the Memory-Based Learning framework. We show how the DOP framework extends the general MBL framework with probabilistic reasoning in order to deal with complex performance phenomena such as syntactic disambiguation. In order to keep this discussion concrete we also analyze the model DOP1, the first instantiation of the DOP framework. Subsequently, we contrast the DOP model to other existing MBL approaches that employ so called "flat" or "intermediate" descriptions as opposed to the hierarchical descriptions used by the DOP model.

7.1 Case-Based Reasoning

In the Machine Learning (ML) literature, e.g. Aamodt & Plaza (1994), Mitchell (1997), various names, e.g. Instance-Based, Case-Based, Memory-Based or Lazy, are used for a paradigm of learning that can be characterized by two properties:

(1) it involves a lazy learning algorithm that does not generalize over the training examples but stores them, and

(2) it involves lazy generalization during the application phase: each new instance is classified (on its own) on basis of its relationship to the stored training examples; the relationship between two instances is examined by means of so called similarity functions.

We will refer to this general paradigm by the term MBL (although the term Lazy Learning, as Aha (1998) suggests, might be more suitable). There are various forms of MBL that differ in several respects. In this study we are specifically interested in the Case-Based Reasoning (CBR) variant of MBL (Kolodner 1993, Aamodt & Plaza 1994).

Case-Based Reasoning differs from other MBL approaches, e.g. k-nearest neighbor methods, in that it does not represent the instances of the task concept [6] as real-valued points in an n-dimensional Euclidean space; instead, CBR methods represent the instances by means of complex symbolic descriptions, e.g. graphs (Aamodt & Plaza 1994, Mitchell 1997). This implies that CBR methods require more complex similarity functions. It also implies that CBR methods view their learning task in a different way than other MBL methods: while the latter methods view their learning task as a classification problem, CBR methods view their learning task as the construction of classes for input instances by reusing parts of the stored classified training-instances.

According to overviews of the CBR literature, e.g. Mitchell (1997), Aha & Wettschereck (1997), there exist various CBR methods that address a wide variety of tasks, e.g. conceptual designs of mechanical devices (Sycara et al. 1992), reasoning about legal cases (Ashley 1990), scheduling and planning problems (Veloso & Carbonell 1993) and mathematical integration problems (Elliot & Scott 1991). Rather than pursuing the infeasible task of contrasting DOP to each of these methods, we will firstly highlight the specific aspects of DOP as an extension to CBR. Subsequently we compare DOP to recent approaches that extend CBR with probabilistic reasoning.

7.2 The DOP framework and CBR

We will show that the first three components of a DOP model as described in the DOP framework of section 3 define a CBR method, and that the fourth component extends CBR with probabilistic reasoning. To this end, we will express each component in CBR terminology and then show how this specifies a CBR system. The first component of DOP, i.e. a formal representation of utterance-analyses, specifies the representation language of the instances and classes in the parsing task, i.e. the so called case description language. The second component, i.e. fragments definition, defines the units that are retrieved from memory when a class (tree) is being constructed for a new instance; the retrieved units are exactly the sub-instances and sub-classes that can be combined into instances and classes. The third component, i.e. definition of combination operations, concerns the definition of the constraints on combining the retrieved units into trees when parsing a new utterance. Together, the latter two components define exactly the retrieval, reuse and revision aspects of the CBR problem solving cycle (Aamodt & Plaza 1994). The similarity measure, however, is not explicitly specified in DOP but is implicit in a retrieval strategy that relies on simple string equivalence. Thus, the first three components of a DOP model specify exactly a simple CBR system for natural language analysis, i.e., a natural language parser. This system is lazy: it does not generalize over the tree-bank until it starts parsing a new sentence, and it defines a space of analyses for a new input sentence simply by matching and combining fragments from the case-base (i.e. tree-bank).

The fourth component of the DOP framework, however, extends the CBR approach for dealing with ambiguities in the definition of the case description language. It specifies how the frequencies of the units retrieved from the case-base define a probability value for the utterance that is being parsed. We may conclude that the four components of the DOP framework define a CBR method that uses possibly recursive case descriptions, string-matching for retrieval of cases, and a probabilistic model for resolving ambiguity. The latter property of DOP is crucial for the task that the DOP framework addresses: disambiguation. Disambiguation differs from the task that mainstream CBR approaches address, i.e. constructing a class for the input instance. Linguistic disambiguation involves classification under an ambiguous definition of the "case description language", i.e., the formal representation of the utterance analyses, which is usually a grammar. Since the fragments (second component of a DOP model) are defined under this "grammar", combining them by means of the combination operations (third component) usually defines an ambiguous CBR system: for classifying (i.e. parsing) a new instance (i.e. sentence), this CBR system may construct more than one analysis (i.e., class). The ambiguity of this CBR system is inherent to the fact that it is often infeasible to construct an unambiguous natural language formal representation of analyses. A DOP model solves this ambiguity when classifying an instance by assigning a probability value to every constructed class in order to select the most probable one. Next we will show how these observations about the DOP framework apply to the DOP1 model for syntactic disambiguation.

7.3 DOP1 and CBR methods

In order to explore the differences between the DOP1 model and CBR methods, we will express DOP1 as an extension to a CBR parsing system. To this end, it is necessary to identify the case-base, the instance-space, the class-space, and the "similarity function" that DOP assumes. In DOP, the training tree-bank contains <string, tree> pairs that represent the classified instances, where string is an instance and tree is a class.

A DOP model memorizes in its case-base exactly the finite set of tree-bank trees. When parsing a new input sentence, the DOP model retrieves from the case-base all subtrees of the trees in its case-base and tries to use them for constructing trees for that sentence. Let us refer to the ordered sequence of symbols that decorate the leaf nodes of a subtree as the frontier of that subtree. Moreover, let us call the frontier of a subtree from the case-base a subsentential-form from the tree-bank. During the retrieval phase, a DOP1 model retrieves from its case-base all pairs <str, st>, where st is a subtree of the tree-bank and the string str is its frontier SSF. These subtrees are used for constructing classes, i.e. trees, for the input sentence using the substitution-operation. This operation enables constrained assemblage of sentences (instances) and trees (classes). The set of sentences and the set of trees that can be assembled from subtrees by means of substitution constitute respectively the instance-space and the class-space of a DOP1 model.

Thus, the instance-space and the class-space of a DOP1 model are defined by the Tree-Substitution Grammar (TSG) that employs the subtrees of the tree-bank trees as its elementary trees; this TSG is a recursive device that defines infinite instance- and class-spaces. However, this TSG, which represents the "runtime" expansion of DOP's case-base, does not generalize over the CFG that underlies the tree-bank (the case description language), since the two grammars have equal string-languages (instance-spaces) and equal tree-languages (class-spaces).

The probabilities that DOP1 attaches to the subtrees in the TSG are induced from the frequencies in the tree-bank and can be seen as subtree weights. Thus, the STSG that a DOP model projects from a tree-bank can be viewed as an infinite runtime case-base containing instance-class-weight triples that have the form <SSF, subtree, probability>.

Task and similarity function

The task implemented by a DOP1 model is disambiguation: the identification of the most plausible tree that the TSG assigns to the input sentence. Syntactic disambiguation is indeed a classification task in the presence of an infinite class-space. For an input sentence, this class-space is firstly limited to a finite set by the (usually) ambiguous TSG: only trees that the TSG constructs for that sentence by combining subtrees from the tree-bank are in the specific class-space of that sentence. Subsequently, the tree with the highest probability (according to the STSG) in this limited space is selected as the most plausible one for the input sentence. To understand the matching and retrieval processes of a DOP1 model, let us consider both steps of disambiguation separately.

In the first step, i.e. parsing, the similarity function that DOP1 employs is a simple recursive string-matching procedure. First, all substrings of the input sentence are matched against SSFs in the case-base (i.e. the TSG) and the subtrees corresponding to the matched SSFs are retrieved; every substring that matches an SSF is replaced by the label of the root node of the retrieved subtree (note that there can be many subtrees retrieved for the same SSF, their roots replace the substring as alternatives). This SSF-matching and subtree-retrieval procedure is recursively applied to the resulting set of strings until the last set of strings does not change.

Technically speaking, this "recursive matching process" is usually implemented as a parsing algorithm that constructs an efficient representation of all trees that the TSG assigns to the input sentence, called the parse-forest that the TSG constructs for that sentence (see section 5).

What is the role of probabilities in the similarity function?

Thus, rather than employing a Euclidean or any other metric to measure the distance between the input sentence and the sentences in the case-base, DOP1 resorts to a recursive matching process where similarity between SSFs is implemented as simple string-equivalence. Beyond parsing, which can be seen as the first step of disambiguation, DOP1 faces the ambiguity of the TSG, which follows from the ambiguity of the CFG underlying the tree-bank (i.e. the case description language definition). This is one important point where DOP1 deviates from mainstream CBR methods that usually employ unambiguous definitions of the case description language, or resort to (often ad hoc) heuristics that give a marginal role to disambiguation.

For natural language processing it is usually not feasible to construct unambiguous grammars. Therefore, the parse-forest that the parsing process constructs for an input sentence usually contains more than one tree. The task of selecting the most plausible tree from this parse-forest, i.e. syntactic disambiguation, constitutes the main task addressed by performance models of syntactic analysis such as DOP1. For disambiguation, DOP1 ranks the alternative trees in the parse-forest of the input sentence by computing a probability for every tree. Subsequently, it selects the tree with the highest probability from this space. It is interesting to consider how the probability of a tree in DOP1 relates to the matching process that takes place during parsing.

Given a parse-tree, we may view each derivation that generates it as a "successful" combination of subtrees from the case-base; to every such combination we assign a "matching-score" of 1. All sentence-derivations that generate a different parse-tree (including the ones that generate a different sentence) receive matching-score 0. The probability of a parse-tree as computed by DOP1 is in fact the expectation value (or mean) of the scores (with respect to this parse-tree) of all derivations allowed by the TSG; this expectation value weighs the score of every derivation by the probability of that derivation. The probability of a derivation is computed as the product of the probabilities of the subtrees that participate in it. Subtree probabilities, in their turn, are based on the frequency counts of the subtrees and are conditioned on the constraint embodied by the tree-substitution combination operation.

This brief description of DOP1 in CBR terminology shows that the following aspects of DOP1 are not present in other mainstream CBR methods: (i) both the instance- and class-spaces are infinite and are defined in terms of a recursive matching process embodied by a TSG-based parser that matches strings by equality, and then retrieves and combines the subtrees associated with the matching strings using the substitution-operation, (ii) the CBR task of constructing a tree (i.e. class) for a input sentence is further complicated in DOP1 by the ambiguity of this TSG, (iii) the "structural similarity function" that most other CBR methods employ is, therefore, implemented in DOP as a recursive process that is complemented by spanning a probability distribution over the instance- and class-spaces in order to facilitate disambiguation, and (iv) the probabilistic disambiguation process in DOP1 is conducted globally over the whole sentence rather than locally on parts of the sentence. Hence we may characterize DOP1 as a lazy probabilistic recursive CBR classifier that addresses the problem of global sentential-level syntactic disambiguation.

7.4 DOP and recent probabilistic extensions to CBR

Recent literature within the CBR approach advocates extending CBR with probabilistic reasoning. Waltz and Kasif (1996) and Kasif et al. (forthcoming) refer to the framework that combines CBR with probabilistic reasoning with the name Memory-Based Reasoning (MBR). Their arguments for this framework are based on the need for systems to be able to adapt to rapidly changing environments "where abstract truths are at best temporary or contingent". This work differs from DOP in at least two important ways: (i) it assumes a non-recursive finite class-space, and (ii) it employs probabilistic reasoning for inducing so called "adaptive distance metrics" (these are distance metrics that automatically change as new training material enters the system) rather than for disambiguation.

These differences imply that this approach does not take note of the specific aspects of the disambiguation task as found in natural language parsing, e.g., the need for recursive symbolic descriptions and that disambiguation lies at the hart of any performance task. The syntactic ambiguity problem, thus, has an additional dimension of complexity next to the dimensions that are addressed by the mainstream ML literature.

7.5 DOP vs. other MBL approaches in NLP

In this section we will concentrate on contrasting DOP to some MBL methods that are used for implementing natural language processing (NLP) tasks. Firstly we briefly address the relatively clear differences between methods based on variations of the k-Nearest Neighbor (k-NN) approach and DOP. Subsequently we discuss more thoroughly the recently introduced Memory-Based Sequence Learning (MBSL) method (Argamon et al. 1998) and how it relates to the DOP model.

7.5.1 k-NN vs. DOP

From the description of CBR methods earlier in this section, it became clear that the main difference between k-NN methods and CBR methods is that the latter employ complex data structures rather than feature vectors for representing cases. As mentioned before, DOP's case description language is further enhanced by recursion and complicated by ambiguity. Moreover, while k-NN methods classify their input in a partitioning of a real-valued multi-dimensional Euclidean space, the CBR methods (including DOP) must construct a class for an input instance. The similarity measures in k-NN methods are based on measuring the distance between the input instance and each of the instances in memory. In DOP, this measure is simplified during parsing to string-equivalence and complicated during disambiguation by a probabilistic ranking of the alternative trees of the input sentence. Of course, it is possible to imagine a DOP model that employs k-NN methods during the parsing phase, so that the string matching process becomes more complex than simple string-equivalence. In fact, a simple version of such an extension of DOP has been studied in Zavrel (1996) -- with inconclusive empirical results due to the lack of suitable training material.

Recently, extensions and enhancements of the basic k-NN methods (Daelemans et al. 1999a) have been applied to limited forms of syntactic analysis (Daelemans et al. 1999b). This work employs k-NN methods for very specific syntactic classification tasks (for instance for recognizing NP's or VP's, and for deciding on PP-attachment or subject/object relations), and then combines these classifiers into shallow parsers. The classifiers carry out their task on the basis of local information; some of them (e.g. subject/object) rely on preprocessing of the input string by other classifiers (e.g. NP- and VP-recognition). This approach has been tested successfully on the individual classification tasks and on shallow parsing, yielding state-of-the-art accuracy results.

This work differs from the DOP approach in important respects. First of all, it does not address the full parsing problem; it is not intended to deal with with arbitrary tree structures derived from an arbitrary corpus, but hardcodes a limited number of very specific syntactic notions. Secondly, the classification decisions (or disambiguation decisions) are based on a limited context which is fixed in advance. Thirdly, the approach employs similarity metrics rather than stochastic modeling techniques. Some of these features make the approach more efficient than DOP, and therefore easier to apply to large tree-banks. But at the same time this method shows clear limitations if we look at its applicability to general parsing tasks, or if we consider the disambiguation accuracy that can be achieved if only local information is taken into account .

7.5.2 Memory-Based Sequence Learning vs. DOP

Memory-Based Sequence Learning (MBSL), described in Aragamon et al. (1998) can be seen as analogous to a DOP model at the level of flat non-recursive linguistic descriptions. It is interesting to pursue this analogy by analysing MBSL in terms of the four components that constitute a DOP model (cf. the end of section 3 above). Since MBSL is a new method that seems closer to DOP1 than all other MBL methods discussed in this volume, we will first summarize how it works before we compare it with DOP1.

Like DOP1, an MBSL system works on the basis of a corpus of utterances annotated with labelled constituent structures. It assumes a different representation of these structures, however: an MBSL corpus consists of bracketed strings. Each pair of brackets delimits the borders of a substring of some syntactic category, e.g., Noun Phrase (NP) or Verb Phrase (VP). For every syntactic category, a separate MBSL system is constructed. Given a corpus containing bracketed strings of part-of-speech tags (pos-tags), an MBSL system stores all [7] the substrings that contain at least one bracket together with their occurrence counts; such substrings are called tiles. Moreover, the MBSL system stores all substrings stripped from the brackets together with their occurrence count. The positive evidence in the corpus for a given tile is computed as the ratio between the occurrence count of the tile to the total occurrence count of the substring obtained by stripping the tile from the brackets.

When an MBSL system is prompted to assign brackets to a new input sentence, it assigns all possible brackets to the sentence and then it computes the positive evidence for every pair of brackets on basis of its stored corpus. To this end, every subsequence of the input sentence surrounded by a (matching) pair of brackets is considered a candidate. A candidate together with the rest of the sentence is considered a situated candidate. To evaluate the positive evidence for a situated candidate, a tiling of that situated candidate is attempted on basis of the tiles that are stored. When tiling a situated candidate, tiles are retrieved from storage and placed such that they cover it entirely. Only tiles of sufficient positive evidence are retrieved for this purpose (a threshold on sufficient evidence is used). To specify how a cover is exactly obtained, it is necessary to define the notion of connecting tiles (with respect to a situated candidate). We say that a tile partially covers a situated candidate if the tile is equivalent to some substring of that situated candidate; the substring is then called a matching substring of the tile. Given a situated candidate and a tile T1 that partially covers it, tile T2 is called connecting to tile T1 iff T2 also partially-covers the situated candidate and the matching substrings of T1 and T2 overlap without being included in each other, or are adjacent to each other in the situated candidate. The shortest substring of a situated candidate that is partially covered by two connecting tiles is said to be covered by the two tiles; we also say that the two tiles constitute a cover of that substring. The notion of a cover is then generalized to a sequence of connecting tiles: a sequence of connecting tiles is an ordered sequence of tiles such that every tile is connecting to the tile that precedes it in that sequence. Hence, a cover of the situated candidate is a sequence of connecting tiles that covers it entirely. Crucially, there can be many different covers of a situated candidate.

The evidence score for a situated candidate is a function of the evidence for the various covers that can be found for it in the corpus. MBSL estimates this score by a heuristic function that combines various statistical measures concerning properties of the covers e.g., number of covers, number of tiles in a cover, size of overlap between tiles, etc. In order to select a bracketing for the input sentence, all possible situated candidates are ranked according to their scores. Starting with the situated candidate with the highest score C, the bracketing algorithm removes all other situated candidates that contain a pair of brackets that overlaps with the brackets in C. This procedure is repeated iteratively until it stabilizes. The remaining set of situated candidates defines a bracketing of the input sentence.

It is interesting to look at MBSL from the perspective of the DOP framework. Let us first consider its representation formalism, its fragment extraction function and its combination operation. The formalism that MBSL employs to represent utterance analyses is a part-of-speech--tagging of the sentences together with a bracketing that defines the target syntactic category. The fragments are the tiles that can be extracted from the training corpus. The combination operation is an operation that combines two tiles such that they connect. We cannot extend this analogy to include the covers, however, because MBSL considers the covers locally with respect to every situated candidate. If MBSL would have employed covers for a whole consistent bracketing of the input sentence, MBSL covers would have corresponded to DOP derivations, and consistent bracketings to parses. Another important difference between MBSL and DOP shows up if we look at the way in which "disambiguation" or pruning of the bracketing takes place in MBSL. Rather than employing a probabilistic model, MBSL resorts to local heuristic functions with various parameters that must be tuned in order to achieve optimal results.

In summary, MBSL and DOP are analogous but nevertheless rather different MBL methods for dealing with syntactic ambiguity. The differences can be summarized by (i) the locally-based (MBSL) vs. globally-based (DOP) ranking strategy of alternative analyses, and (ii) the ad hoc heuristics for computing scores (MBSL) vs. the stochastic model (DOP) for computing probabilities.

Note also that the combination operation employed by the MBSL system allows a kind of generalization over the tree-bank that is not possible in DOP1. Because MBSL allows tiling situated candidates using tiles that contain one bracket (either a left or a right bracket) the matching pairs of brackets that result from a series of connecting tiles may delimit a string of part-of-speech-tags that cannot be constructed by nested pairs of matching brackets from the tree-bank (which is a kind of substitution-operation of bracketed strings).

In contrast to MBSL, DOP1's tree substitution-operation generates only SSFs that can be obtained by nesting SSFs from the tree-bank under the restrictive constraints of the substitution-operation. This implies that each pair of matching brackets that corresponds to an SSF is a matching pair of brackets that can be found in the tree-bank. DOP1 generates exactly the same set of trees as the CFG underlying the tree-bank, while MBSL generalizes beyond the string-language and the tree-language of this CFG. It is not obvious, however, that MBSL operates in terms of the most felicitous representation of hierarchic surface structure, and one may wonder to what extent the generalizations produced in this way are actually useful.

Before we close off this section, we should emphasize that DOP-models do not necessarily lack all generalization power. Some extensions of DOP1 have been developed that learn new subtrees (and SSFs) by allowing mismatches between categories (in particular between SSFs and part-of-speech-tags). For instance, Bod (1995) discusses a model which assigns non-zero probabilities to unobserved lexical items on the basis of Good-Turing estimation. Another DOP-model (LFG-DOP) employs a corpus annotated with LFG-structures, and allows generalization over feature values (Bod & Kaplan 1998). We are currently investigating the design of DOP-models with more powerful generalization capabilities.

8. Conclusion

In this paper we focused on the Memory-Based aspects of the Data Oriented Parsing (DOP) model. We argued that disambiguation is a central element of linguistic processing that can be most suitably modelled by a memory-based learning model. Furthermore, we argued that this model must employ linguistic grammatical descriptions and that it should employ probabilities in order to account for the psycholinguistic observations concerning the central role that frequencies play in linguistic processing. Based on these motivations we presented the DOP model as a probabilistic recursive Memory-Based model for linguistic processing. We discussed some computational aspects of a simple instantiation of it, called DOP1, that aims specifically at syntactic disambiguation.

We also summarized some of our empirical and experimental observations concerning DOP1 that are specifically related to its Memory-Based nature. We conclude that these observations provide convincing evidence for the hypothesis that the structural units for language processing should not be limited to a minimal set of grammatical rules but that they must be defined in terms of a (redundant) space of linguistic relations that are encountered in an explicit "memory" or "case-base" that represents linguistic experience. Moreover, although many of our empirical observations support the argument for a purely memory-based approach, we encountered other empirical observations that exhibit the strong tension that exists between this argument and various factors that are encountered in practice e.g. data-sparseness. We may conclude, however, that our empirical observations do support the idea that "forgetting exceptions is harmful" (Van den Bosch & Daelemans 1998).

Furthermore, we analyzed the DOP model within the MBL paradigm and contrasted it to other MBL approaches within NLP and outside it. We concluded that despite the many similarities between DOP and other MBL models, there are major differences. For example, DOP1 distinguishes itself from other MBL models in that (i) it deals with a classification task involving infinite instance spaces and class spaces described by an ambiguous recursive grammar, and (ii) it employs a disambiguation facility based on a stochastic extension of the syntactic case-base.


Endnotes

1. We employed a cleaned-up version of this corpus in which mistagged words had been corrected by hand, and analyses with so-called pseudo-attachments had been removed.
   
   
2. Bod (1998a) also presents experiments with extensions of DOP1 that generalize over the corpus fragments. DOP1 cannot cope with unknown words.
   
   
3. Bod (1995, 1998a) shows how to extend the model to overcome this limitation.
   
   
4. The experiments in Sima'an (1999) concern a comparison between DOP1 and a new model, called Specialized DOP (SDOP). Since this comparison is not the main issue here, we will summarize the results concerning the DOP1 model only. However, it might be of interest here to mention the conclusions of the comparison. In short, the SDOP model extends the DOP1 model with automatically inferred subtree-selection criteria. These criteria are determined by a new learning algorithm that specializes the annotation of the training tree-bank to the domain of language use represented by that tree-bank. The SDOP models acquired from a tree-bank are substantially smaller than the DOP1 models. Nevertheless, Sima'an (1999) shows that the SDOP models are at least as accurate and have the same coverage as DOP1 models.
   
   
5. The SRI-ATIS tree-bank was generously made available for these experiments by SRI International, Cambridge (UK).
   
   
6. A concept is a function; members of its domain are called instances and members of its range are called classes. The task or target concept is the function that the learning process tries to estimate.
   
   
7. In fact only limited context is allowed around a bracket, which means that not all of the substrings in the corpus are stored.
   
   

References

A. Aamodt and E. Plaza, 1994. "Case-Based Reasoning: Foundational issues, methodological variations and system approaches", AI Communications, 7. 39-59.

D. Aha, 1998. "The Omnipresence of Case-Based Reasoning in Science and Application", Knowledge-Based Systems 11(5-6), 261-273.

D. Aha and D. Wettschereck, 1997. "Case-Based Learning: Beyond Classification of Feature Vectors", ECML-97 invited paper. Also in MLnet ECML'97 workshop. MLnet News, 5:1, 8-11.

S. Abney, 1996. "Statistical Methods and Linguistics." In: Judith L. Klavans and Philip Resnik (eds.): The Balancing Act. Combining Symbolic and Statistical Approaches to Language. Cambridge (Mass.): MIT Press, pp. 1-26.

H. Alshawi, editor, 1992. The Core Language Engine, Boston: MIT Press.

H. Alshawi and D. Carter, 1994. "Training and Scaling Preference Functions for Disambiguation", Computational Linguistics.

K. Ashley, 1990. Modeling legal argument: Reasoning with cases and hypotheticals, Cambridge, MA: MIT Press.

M. van den Berg, R. Bod and R. Scha, 1994. "A Corpus-Based Approach to Semantic Interpretation", Proceedings Ninth Amsterdam Colloquium, Amsterdam, The Netherlands.

E. Black, S. Abney, D. Flickenger, C. Gnadiec, R. Grishman, P. Harrison, D. Hindle, R. Ingria, F. Jelinek, J. Klavans, M. Liberman, M. Marcus, S. Roukos, B. Santorini and T. Strzalkowski, 1991. "A Procedure for Quantitatively Comparing the Syntactic Coverage of English", Proceedings DARPA Speech and Natural Language Workshop, Pacific Grove, Morgan Kaufmann.

A. van den Bosch and W. Daelemans, 1998. "Do not forget: Full memory in memory-based learning of word pronunciation", Proceedings of NeMLaP3/CoNLL98.

E. Black, J. Lafferty and S. Roukos, 1992. "Development and Evaluation of a Broad-Coverage Probabilistic Grammar of English-Language Computer Manuals", Proceedings ACL'92, Newark, Delaware.

R. Bod, 1992. "A Computational Model of Language Performance: Data Oriented Parsing", Proceedings COLING'92, Nantes.

R. Bod, 1993a. "Using an Annotated Language Corpus as a Virtual Stochastic Grammar", Proceedings AAAI'93, Morgan Kauffman, Menlo Park, Ca.

R. Bod, 1993b. "Monte Carlo Parsing". Proceedings of the Third International Workshop on Parsing Technologies. Tilburg/Durbuy.

R. Bod, 1995. Enriching Linguistics with Statistics: Performance Models of Natural Language, Ph.D. thesis, ILLC Dissertation Series 1995-14, University of Amsterdam.

R. Bod, 1998a. Beyond Grammar, CSLI Publications / Cambridge University Press, Cambridge.

R. Bod, 1998b. "Spoken Dialogue Interpretation with the DOP Model", Proceedings COLING-ACL'98, Montreal, Canada.

R. Bod and R. Kaplan, 1998. "A Probabilistic Corpus-Driven Model for Lexical-Functional Analysis", Proceedings COLING-ACL'98, Montreal, Canada.

R. Bod and R. Scha, 1996. Data-Oriented Language Processing. An Overview. Technical Report LP-96-13. Institute for Logic, Language and Computation, University of Amsterdam.

R. Bod and R. Scha, 1997. "Data-Oriented Language Processing." In S. Young and G. Bloothooft (eds.) Corpus-Based Methods in Language and Speech Processing, Kluwer Academic Publishers, Boston. 137-173.

R. Bonnema, 1996 Data-Oriented Semantics. Master's Thesis, Department of Computational Linguistics (Institute for Logic, Language and Computation).

R. Bonnema, R. Bod and R. Scha, 1997. "A DOP Model for Semantic Interpretation", Proceedings 35th Annual Meeting of the ACL / 8th Conference of the EACL, Madrid, Spain.

C. Brew, 1995. "Stochastic HPSG", Proceedings European chapter of the ACL'95, Dublin, Ireland.

T. Briscoe and J. Carroll, 1993. "Generalized Probabilistic LR Parsing of Natural Language (Corpora) with Unification-Based Grammars", Computational Linguistics 19(1), 25-59.

J. Carroll and D. Weir, 1997. "Encoding Frequency Information in Lexicalized Grammars", Proceedings 5th International Workshop on Parsing Technologies, MIT, Cambridge (Mass.).

D. Carter, 1997. "The TreeBanker: a Tool for Supervised Training of Parsed Corpora", Proceedings of the workshop on Computational Environments for Grammar Development and Linguistic Engineering, ACL/EACL'97, Madrid, Spain.

T. Cartwright and M. Brent, 1997. "Syntactic categorization in early language acquisition: formalizing the role of distributional analysis." Cognition 63, pp. 121-170.

J. Chappelier and M. Rajman, 1998. "Extraction stochastique d'arbres d'analyse pour le modèle DOP", Proceedings TALN 1998, Paris, France.

E. Charniak, 1996. "Tree-bank Grammars", Proceedings AAAI'96, Portland, Oregon.

E. Charniak, 1997. "Statistical Techniques for Natural Language Parsing", AI Magazine.

N. Chomsky, 1966. Cartesian Linguistics. A Chapter in the History of Rationalist Thought. New York: Harper & Row.

K. Church and R. Patil, 1983. Coping with Syntactic Ambiguity or How to Put the Block in the Box on the Table, MIT/LCS/TM-216.

J. Coleman and J. Pierrehumbert, 1997. "Stochastic Phonological Grammars and Acceptability", Proceedings Computational Phonology, Third Meeting of the ACL Special Interest Group in Computational Phonology, Madrid, Spain.

M. Collins, 1996. "A new statistical parser based on bigram lexical dependencies", Proceedings ACL'96, Santa Cruz (Ca.).

M. Collins, 1997. "Three generative lexicalised models for statistical parsing", Proceedings EACL-ACL'97, Madrid, Spain.

W. Daelemans, A. van den Bosch and J. Zavrel, 1999a. "Forgetting exceptions is harmful in language learning." Machine Learning 34, 11-41.

W. Daelemans, S. Buchholz and J. Veenstra, 1999b. "Memory-Based Shallow Parsing." To appear in CoNLL '99.

G. DeJong, 1981. "Generalizations based on explanations", Proceedings of the Seventh International Joint Conference on Artificial Intelligence.

G. DeJong and R. Mooney, 1986. "Explanation-Based Generalization: An alternative view", Machine Learning 1:2, 145-176.

J. Eisner, 1997. "Bilexical Grammars and a Cubic-Time Probabilistic Parser", Proceedings Fifth International Workshop on Parsing Technologies, Boston, Mass.

T. Elliot and P. Scott, 1991. "Instance-based and generalization-based learning procedures applied to solving integration problems", Proceedings of the 8th Conference of the Society for the Study of AI, Leeds, UK: Springer.

G. Fenk-Oczlon, 1989. "Word frequency and word order in freezes", Linguistics 27, 517-556.

K. Fu, 1982. Syntactic Pattern Recognition and Applications, Prentice-Hall.

J. Goodman, 1996. "Efficient Algorithms for Parsing the DOP Model", Proceedings Empirical Methods in Natural Language Processing, Philadelphia, PA.

J. Goodman, 1998. Parsing Inside-Out, Ph.D. thesis, Harvard University, Mass.

J. Hammersley and D. Handscomb, 1964. Monte Carlo Methods, Chapman and Hall, London.

F. van Harmelen and A. Bundy, 1988. "Explanation-Based Generalization = Partial Evaluation", Artificial Intelligence 36, 401-412.

I. Hasher and W. Chromiak, 1977. "The processing of frequency information: an automatic mechanism?", Journal of Verbal Learning and Verbal Behavior 16, 173-184.

I. Hasher and R. Zacks, 1984. "Automatic Processing of Fundamental Information: the case of frequency of occurrence", American Psychologist 39, 1372-1388.

C. Hemphill, J. Godfrey and G. Doddington, 1990. "The ATIS spoken language systems pilot corpus". Proceedings DARPA Speech and Natural Language Workshop, Hidden Valley, Morgan Kaufmann.

L. Jacoby and L. Brooks, 1984. "Nonanalytic Cognition: Memory, Perception and Concept Learning", G. Bower (ed.), Psychology of Learning and Motivation (Vol. 18, 1-47), San Diego: Academic Press.

F. Jelinek, J. Lafferty and R. Mercer, 1990. Basic Methods of Probabilistic Context Free Grammars, Technical Report IBM RC 16374 (#72684), Yorktown Heights.

M. Johnson, 1995. Personal communication.

C. Juliano and M. Tanenhaus, 1993. "Contingent Frequency Effects in Syntactic Ambiguity Resolution", Fifteenth Annual Conference of the Cognitive Science Society, 593-598, Hillsdale, NJ.

S. Kasif, S. Salzberg, D. Waltz, J. Rachlin and D. Aha, forthcoming. "A Probabilistic Framework for Memory-Based Reasoning." To appear in Artificial Intelligence.

D. Kausler and J. Puckett, 1980. "Frequency Judgments and Correlated Cognitive Abilities in Young and Elderly Adults", Journal of Gerontology 35, 376-382.

M. Kay, 1980. Algorithmic Schemata and Data Structures in Syntactic Processing. Report CSL-80-12, Xerox PARC, Palo Alto, Ca.

J. Kolodner, 1993. Case-Based Reasoning, Morgan Kauffman, Menlo Park.

M. MacDonald, N. Pearlmutter and M. Seidenberg, 1994. "Lexical Nature of Syntactic Ambiguity Resolution", Psychological Review 101, 676-703.

M. Marcus, B. Santorini and M. Marcinkiewicz, 1993. "Building a Large Annotated Corpus of English: the Penn Treebank", Computational Linguistics 19(2).

W. Martin, K. Church and R. Patil, 1987. "Preliminary Analysis of a Breadth-first Parsing Algorithm: Theoretical and Experimental Results", in: L. Bolc (ed.), Natural Language Parsing Systems, Springer Verlag, Berlin.

T. Mitchell, 1997. Machine Learning, McGraw-Hill Series in Computer Science.

D. Mitchell, F. Cuetos and M. Corley, 1992. "Statistical versus Linguistic Determinants of Parsing Bias: Cross-linguistic Evidence", Fifth Annual CUNY Conference on Human Sentence Processing, New York, NY.

N. Pearlmutter and M. MacDonald, 1992. "Plausibility and Syntactic Ambiguity Resolution", Proceedings 14th Annual Conf. of the Cognitive Society.

M. Rajman, 1995. Apports d'une approche a base de corpus aux techniques de traitement automatique du langage naturel, Ph.D. Thesis, École Nationale Supérieure des Télécommunications, Paris.

P. Resnik, 1992. "Probabilistic Tree-Adjoining Grammar as a Framework for Statistical Natural Language Processing", Proceedings COLING'92, Nantes.

G. Sampson, 1986. "A Stochastic Approach to Parsing", Proceedings COLING'86, Bonn, Germany.

R. Scha, 1990. "Language Theory and Language Technology; Competence and Performance" (in Dutch), in Q.A.M. de Kort & G.L.J. Leerdam (eds.), Computertoepassingen in de Neerlandistiek, Almere: Landelijke Vereniging van Neerlandici (LVVN-jaarboek). [English translation]

R. Scha, 1992. "Virtual Grammars and Creative Algorithms" (in Dutch), Gramma/TTT 1(1). [English translation]

Y. Schabes, 1992. "Stochastic Lexicalized Tree-Adjoining Grammars", Proceedings COLING'92, Nantes.

S. Schütz, 1996. Part-of-Speech Tagging: Rule-Based, Markovian, Data-Oriented. Master's Thesis, University of Amsterdam, The Netherlands.

S. Sekine and R. Grishman, 1995. "A Corpus-based Probabilistic Grammar with Only Two Non-terminals", Proceedings Fourth International Workshop on Parsing Technologies, Prague, Czech Republic.

K. Sima'an, R. Bod, S. Krauwer and R. Scha, 1994. "Efficient Disambiguation by means of Stochastic Tree Substitution Grammars", Proceedings International Conference on New Methods in Language Processing, UMIST, Manchester, UK.

K. Sima'an, 1995. "An optimized algorithm for Data Oriented Parsing", Proceedings International Conference on Recent Advances in Natural Language Processing, Tzigov Chark, Bulgaria.

K. Sima'an, 1996a. "An optimized algorithm for Data Oriented Parsing", in R. Mitkov and N. Nicolov (eds.), Recent Advances in Natural Language Processing 1995, volume 136 of Current Issues in Linguistic Theory. John Benjamins, Amsterdam.

K. Sima'an, 1996b. "Computational Complexity of Probabilistic Disambiguation by means of Tree Grammars", Proceedings COLING-96, Copenhagen, Denmark. (cmp-lg/9606019)

K. Sima'an, 1997. "Explanation-Based Learning of Data-Oriented Parsing", in T. Ellison (ed.) CoNLL97: Computational Natural Language Learning, ACL'97, Madrid, Spain.

K. Sima'an, 1999. Learning Efficient Disambiguation. Ph.D. Thesis, University of Utrecht. ILLC Dissertation Series nr. 1999-02. Utrecht / Amsterdam, March 1999.

B. Srinivas and A. Joshi, 1995. "Some novel applications of explanation-based learning to parsing lexicalized tree-adjoining grammars", Proceedings ACL'95, Cambridge (Mass.).

P. Suppes, 1970. "Probabilistic Grammars for Natural Languages", Synthese 22.

K. Sycara, R. Guttal, J. Koning, S. Narasimhan and D. Navinchandra, 1992. "CADET: A case-based synthesis tool for engineering design", International Journal of Expert Systems, 4(2), 151-188.

D. Tugwell, 1995. "A State-Transition Grammar for Data-Oriented Parsing", Proceedings EACL'95, Dublin, Ireland.

M. Veloso and J. Carbonell, 1993. "Derivational analogy in PRODIGY: Automating case acquisition, storage, and utilization", Machine Learning, 10, 249-279.

A. Viterbi, 1967. "Error bounds for convolutional codes and an asymptotically optimum decoding algorithm", IEEE Trans. Information Theory, IT-13, 260-269.

D. Waltz and S. Kasif, 1996. "On Reasoning from Data," Computing Surveys.

T. Winograd, 1983. Language as a Cognitive Process. Volume I: syntax. Reading (Mass.).

J. Zavrel, 1996. Lexical Space: Learning and Using Continuous Linguistic Representations. Master's Thesis, Department of Philosophy, Utrecht University, The Netherlands.

.