Computationele Esthetica

Remko Scha en Rens Bod

Bestaande formele theorieën die van visuele patronen de "schoonheidcoëfficiënt" berekenen, doen geen recht aan de complexiteit van de esthetische ervaring. Om subtielere theorieën te kunnen ontwikkelen, moet er eerst aandacht besteed worden aan formele modellen van de menselijke waarnemings-processen.

De esthetische ervaring is een van de meest raadselachtige zij-effekten van de menselijke waarneming. Toch zijn er in de afgelopen decennia een aantal mathematische modellen ontwikkeld die aan visuele patronen een "schoonheids-coëfficient" toekennen -- een getal dat zou moeten correleren met de door het patroon opgeroepen mate van esthetisch genoegen. Zulke theorieën lijken wat naïef omdat ze zich toespitsen op een kwantitatief en absoluut schoonheids-oordeel. Ze gaan voorbij aan de kwalitatieve aspekten van specifieke esthetische ervaringen, en leggen geen rekenschap af van de contekst-afhankelijkheid en de variabiliteit van schoonheidsoordelen. Toch is het wel interessant om eens te kijken naar de werking van deze overdreven simplistische schoonheidberekeningen; misschien kunnen ze, in kombinatie met andere ideeën uit waarnemingspsychologie en computationele taalkunde, wel degelijk een aanknopingspunt vormen voor de ontwikkeling van adekwatere formele modellen.

Kant en de schoonheidservaring.

De beste analyse van het esthetische is nog steeds die van Immanuel Kant. Hij zag de schoonheidservaring als het bewustzijn van een psychologisch proces: het plezierig gewaarworden van het harmonisch karakter van het vrije spel van onze cognitieve vermogens. Als Kant hier gelijk in heeft, is het natuurverschijnsel of kunstvoorwerp dat ons in verrukking brengt in feite slechts een aanleiding. Dan moeten we, om het esthetische te begrijpen, in de eerste plaats de waarnemings-processen begrijpen; die zitten blijkbaar zo in elkaar dat ze zich soms, geholpen door de eigenschappen van hun input, kunnen boot-strappen tot schoonheidservaringen.

In Kant's opvatting is de objektiviteit van esthetische oordelen niet vanzelfsprekend: hij konstrueerde die als een intersubjektiviteit -- als een indirekt gevolg van de hoge mate van gelijkenis die er toch altijd bestaat tussen de cognitieve machinerieën van verschillende personen. De validiteit van volstrekt willekeurige individuele smaak-oordelen meende Kant dan toch te kunnen betwisten door de "beter ontwikkelde" smaak als algemene norm te stellen. Latere filosofen hebben er vaak op gewezen dat dit een van de zwakkere plekken is in Kant's verhaal. Een psychologische schoonheidsnotie is noodzakelijkerwijs subjektief, en zeker niet normatief.

Een schoonheidsbegrip dat niet meer doet dan objekten klassificeren als mooi dan wel minder mooi, neutraal, of lelijk, moet tegen de achtergrond van het bovenstaande als naïef worden gezien. Toch is het zo'n schoonheidsbegrip dat ten grondslag ligt aan alle tot nu toe voorgestelde formele schoonheidstheorieën. Misschien moeten we daar niet verbaasd over zijn. Over allerlei veel banalere aspekten van de waarneming bestaan ook nog geen formeel gearticuleerde inzichten; het is daarom niet realistisch om nu al mathematische theorieën te verwachten die alle complexiteiten van het esthetische onder ogen zien.

Dat de bestaande formele schoonheidstheorieën een beetje karikaturaal zijn, moet dus niet per se als een bezwaar gezien worden. Als ze bepaalde aspekten van het esthetische analyseren op een manier die voor uitbreiding of verfijning vatbaar is, dan kan dat op zichzelf al interessant zijn. In dit artikel nemen we enkele van deze theorieën vanuit zo'n gezichtspunt onder de loep. Vervolgens komen we dan terug op de vraag wat een adekwatere computationele modellering van de esthetische processen zou moeten behelzen.

Birkhoff en de harmonie.

De twintigste-eeuwse formele schoonheidstheorieën sluiten nauw aan bij eerdere informele theorieën die in de schoonheidservaring vooral het gevoel van harmonie benadrukten, en dat gevoel dan verklaarden uit onze resonantie met de harmonische eigenschappen van het beschouwde objekt -- met self-similarities, symmetrieën, en eenvoudige proporties in de verschijningsvorm van dat objekt. In deze opvatting is de schoonheid in wezen wiskundig van aard, en de antieke Pythagoreërs waren niet de enigen die dat ook expliciet zo zagen. Zo beschreef G.W. Leibniz het kunstgenot als het onbewust berekenen van getalsverhoudingen -- tussen tijdsintervallen, in het geval van muziek, of tussen afmetingen, in het geval van beeldende kunst en architektuur.

De Amerikaanse wiskundige George David Birkhoff deed in 1928 de eerste pogingen om zulke noties te formaliseren. Hij introduceerde het begrip Esthetische Maat (M), gedefinieerd als het quotient van Orde (O) en Complexiteit (C): M = O/C. De Complexiteit is daarbij grofweg het aantal elementen waaruit een beeld is samengesteld; de orde is een maat voor het aantal regelmatigheden dat in het beeld wordt aangetroffen. Voor verschillende kunstgenres heeft Birkhoff specifieke regels aangegeven om Orde en Complexiteit daadwerkelijk exact te berekenen.

Zo definieert hij voor veelhoeken de Complexiteit als het aantal zijden, en laat hij de getalwaarde voor Orde ondermeer afhangen van de aanwezigheid van vertikale symmetrie, van puntsymmetrie, en van mechanische stabiliteit ten opzichte van een imaginair horizontaal grondvlak. Figuur 1 geeft voor enkele veelhoeken de berekende waarden voor de Esthetische Maat. Zoals te voorzien was, gaan de hoogste scores naar patronen met zo weinig mogelijk onderdelen en zoveel mogelijk symmetrie. Het vierkant komt als winnaar uit de bus.

 

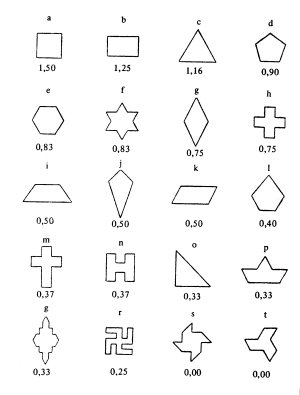
Figuur 1:
De esthetische maat van enkele veelhoeken
volgens Birkhoff's formule: M = O/C.
(Naar: G.D. Birkhoff)

Birkhoff's formule lijkt dus niet zozeer het idee "schoonheid" te formaliseren, als wel het idee "geordendheid". Misschien is het mogelijk om de geordendheids-notie te vereenzelvigen met de schoonheids-notie, maar dat is dan wel een nogal specifieke esthetische keuze. Kunststromingen als NUL en minimal art hebben zo'n soort keuze inderdaad gemaakt. Ook in de konstruktivistische traditie speelt deze visie een belangrijke rol: "If a picture works out without a remainder, that means that all its elements are logically related to each other; it means that each color corresponds to every other, each form to every other, each form to every color and both form and color to their contents. It means ultimately: that its structure is homogeneous, from conception to perception." (Gerstner, 1981, p.35.)

Birkhoff was wel degelijk geïnteresseerd in de empirische validiteit van zijn theorie. Hij heeft daarom ook wel eens veelhoeken voorgelegd aan studenten, en hun schoonheidsoordelen vergeleken met die van zijn formule. Hij heeft de details van deze experimenten nooit bekend gemaakt, maar hij was wel tevreden over de uitkomsten ("the judgments of students seem to indicate the validity of the formula"). Recentere psychologische experimenten leverden echter slechts een zwakke correlatie op tussen Birkhoff's maat en de feitelijke schoonheidsoordelen van proefpersonen. Deze kontekst-afhankelijkheid van de esthetische oordelen is niet verwonderlijk: er is geen enkele reden om te veronderstellen dat mensen één gefixeerde schoonheidsnotie in hun hoofd hebben, die met een willekeurig laboratorium-experiment te aktiveren is. Het is veel waarschijnlijker dat mensen, afhankelijk van de situatie, input-patronen op allerlei verschillende manier kunnen klassificeren, die allemaal iets met de esthetische dimensie van de waarneming te maken hebben.

Voor een ander domein, een klasse van Chinese vazen, heeft Birkhoff de getalwaarde voor Orde op een heel andere manier gedefinieerd. Hij gaat hierbij uit van de tweedimensionale projectie van de vaas. Door de buigpunten en extrema in de omtrek van de vaas trekt trekt hij vervolgens raaklijnen, horizontale lijnen en vertikale lijnen, en telt dan hoe vaak snijpunten van deze lijnen met elkaar samenvallen, en hoe vaak paren van zulke punten dezelfde afstand ten opzichte van elkaar hebben. De volgende figuren laten zien hoe Birkhoff bij de vaas met de hoogste Esthetische Maat uitkomt.

Figuur 2. Links: de esthetische maat van enkele vaasvormen volgens Birkhoff's formule: M=O/C.
Rechts: De 'ideale vaas' volgens Birkhoff. (Naar: G.D. Birkhoff)

De formule lijkt zich nu interessanter te gedragen. De Esthetische Maat correleert nu wel met een eigenschap van "elegantie", in plaats van met een triviale geordendheids-eigenschap. Dat komt omdat de klasse van te vergelijken objekten nu op een andere (en beperktere) wijze is gedefinieerd: de verschillende vaasvormen zijn allemaal distorties van één basisvorm. De vormen kunnen dienovereenkomstig nauwkeuriger met elkaar worden vergeleken, in termen van de hoeveelheid extra interne samenhang die ze vertonen. Opnieuw vinden we op die manier de singulariteiten in een ruimte van mogelijkheden, maar nu zijn die minder voorspelbaar.

De als "mooi" geklassificeerde exemplaren krijgen nu inderdaad iets van de "organische eenheid" die vaak als een kenmerk van het geslaagde kunstwerk wordt gezien: "Every element in a work of art is so involved with other elements in the making of the virtual object, the work, that when it is altered (as it may be -- artists make many alterations after the composition is well under way) one almost always has to follow up the alteration in several directions, or simply sacrifice some desired effects. [...] This many-sided involvement of every element with the total fabric of the poem is what gives it a semblance of organic structure; like living substance, a work of art is inviolable; break its elements apart, and they no longer are what they were -- the whole image is gone." (Langer, 1957, pp. 55-57.)

Birkhoff heeft zijn formule ook in detail uitgewerkt voor het klank-aspekt van poëzie, en voor melodieën. Die uitwerkingen zullen we niet in detail bespreken, en het is wel de moeite waard om op te merken dat het op grond van het bovenstaande allerminst voorspelbaar is hoe ze er uit zouden moeten zien, en ook niet, wat voor schoonheidsintuïtie er dan geformaliseerd zou worden. Dat verraadt wel een zwak punt in Birkhoff's "theorie": voor elk genre van input-objekten moeten weer nieuwe regels geformuleerd worden, en de schoonheidsnotie die door Birkhoff's formule belichaamd wordt kan daarmee telkens weer wat verschuiven.

Bense en de Informatie-Theorie.

Het zal geen verbazing wekken dat er onderzoekers geweest zijn die, met Birkhoff's idee als uitgangspunt, geprobeerd hebben een algemenere, meer-omvattende theorie te ontwikkelen. Dat is met name een groep literatuurtheoretici in het Duitsland van de jaren vijftig geweest, onder aanvoering van Max Bense. Het werk van deze groep heeft geleid tot de informatie-esthetica -- een aanzet voor een Birkhoff-achtig model van het schoonheidsoordeel, geformuleerd in termen ontleend aan Claude Shannon's toen nog nieuwe informatie-theorie.

Men gaat daarbij uit van Birkhoff's oorspronkelijke formule: M = O/C. De definitie van de Complexiteit van een input-patroon wordt dan min of meer ontleend aan Shannon's Informatie-begrip: als een input-patroon n binaire keuzes specificeert uit de klasse van mogelijke patronen, dan is de Complexiteit = n . Om die complexiteit dan ook zonder omwegen te kunnen uitrekenen, maakt men de aanname dat een input-patroon altijd beschreven kan worden als een twee-dimensionaal raster van diskrete symbolen uit een tevoren bekend repertoire. Als dat repertoire k symbolen bevat die allemaal een gelijke a priori kans hebben om op te treden, heeft elk symbool een informatie-inhoud die overeenkomt met 2log k binaire keuzes. De informatie-inhoud H1 van een m bij n raster is dan: n * m * 2log k, en dat is ook de waarde die men dan toekent aan de Complexiteit C van zo'n patroon .

Figuur 3: Enkele rasterpatronen in volgorde van toenemende ordelijkheid: steeds grotere 'supertekens'. (Naar: Gunzenhäuser, 1975)

Om ook te komen tot een soortgelijke uitwerking van Birkhoff's Orde-notie, merken we op dat ordelijkheid correspondeert met de mogelijkheid om grotere strukturen waar te nemen. Als we die grotere strukturen nu ook weer kunnen beschouwen als diskrete "supersymbolen" binnen een bekend repertoire, dan kunnen we ook de informatie-inhoud H2 berekenen van het patroon zoals beschreven in termen van deze supersymbolen. Indien niet alle combinaties van elementaire symbolen als legitieme distinkte supersymbolen beschouwd worden, is de nieuwe kodering zuiniger dan de oorspronkelijke, en is H2 dus kleiner dan H1. De beschrijving in termen van supersymbolen levert een "Ordnungsgewinn" op. De mate van ordelijkheid van het patroon komt overeen met het verschil tussen de informatie-inhoud van de oorspronkelijke kodering en de informatie-inhoud van de uiteindelijke kodering: H1 - H2. En Birkhoff's formule voor de Esthetische Maat wordt dus: M = (H1 - H2)/H1.

Het idee van Bense et al. blijft dus redelijk dicht bij Birkhoff's oorspronkelijke intuïtie, maar suggereert toch een ietwat ander model van het waarnemings-proces. Bij Birkhoff volgt de geordendheids-ervaring onmiddellijk uit het waarnemen van een relatief groot aantal regelmatigheden; in de informatie-esthetiek volgt die geordendheids-ervaring uit de transitie tussen een initiële kodering van de input (geformuleerd in termen van individuele lijnstukken, woorden of tonen) en de zuinigere herkodering ervan (in termen van abstraktere noties) die na enige reflektie tot stand komt.

Aldus beschouwd, korrespondeert de informatie-esthetische formule wel met een vaker geopperde gedachte over de rol die de perceptuele eenheid van het kunstwerk speelt in het totstandkomen van de schoonheidservaring: "Initially, the details of the work seem to be just there, and we may seem free to conjoin them this way or that, whichever way we please. Yet if we dwell with the art work, and if this work is genuine, it comes to crystallize into a whole: the parts fit together and we discern a certain necessity in their cohesion. And since we are now guided by this sense of necessity, we are forced to discard our "old" freedom. But we do not experience this necessity as a mere external constraint. Rather it comes to us as a liberation, a release: we are freed from the fragmentariness of mere detail and come to be at home in a rich whole. It is not that we discard or obliterate the details, but in standing beyond their fragmentariness we ourselves are freed from fragmentation. Such a "standing beyond" which unites and preserves the internal details of a complex whole, in fact, makes the art work an aesthetic concretion of Hegel's general principle of Aufhebung". (Desmond, 1986, p. 64.)

De informatie-esthetica van Bense et al. is echter niet algemener dan Birkhoff's theorie. Hij kan beter gezien worden als een toevoeging aan Birkhoff's lijst van regels voor specifieke genres. De informatie-esthetica geeft regels om Complexiteit en Orde te berekenen voor een heel specifiek soort beeld: een raster dat samengesteld is uit diskrete symbolen, afkomstig uit een expliciet gespecificeerd eindig repertoire. Er is een suggestie van algemeenheid, omdat technisch gesproken alle beelden bij benadering zo gezien kunnen worden -- als we ze opgebouwd denken uit pixels. Maar die suggestie is niet juist, want voor de meeste beelden die we in de praktijk tegenkomen is een opbouw uit naast elkaar gestelde diskrete elementen niet de perceptief relevante analyse.

De informatie-esthetica erft ook Birkhoff's voorkeur voor minimalistische strukturen. Hoe eenvoudiger het beeld, hoe kompakter de kodering uiteindelijk kan worden, en hoe groter het resulterende "Ordnungsgewinn". Maar juist bij rasterbeelden is het heel duidelijk dat de voorkeur voor "totale orde" tot verkeerde resultaten leidt. Het is al vaak opgemerkt dat een intuïtieve schoonheidsmaat niet alleen een nul-waarde zou moeten krijgen wanneer een patroon te complex is om er enige ordening in waar te nemen (random patronen: figuur 4 linksboven), maar ook wanneer een patroon reeds tot in de perfekte banaliteit geordend is (figuur 4 rechtsonder). Voor de perceptie zijn totale wanorde en totale orde ongeveer identiek. De maximale waarde voor de Esthetische Maat zouden we dus ergens tussen deze twee polen moeten aantreffen.

Figuur 4: Enkele rasterpatronen in volgorde van toenemende ordelijkheid. (Naar: Gunzenhäuser, 1975)

En er is nog een ander probleem met de informatie-esthetische maat: de berekening gaat uit van een tevoren bekend repertoire van supertekens. Maar veel vormen van ordelijkheid, en niet de lelijkste, gebruiken supertekens die door het kunstwerk zelf gedefinieerd worden. Een bepaalde kombinatie van elementaire tekens kan als een superteken funktioneren, enkel en alleen omdat hij (in letterlijke of getransformeerde vorm) vaker in het totale patroon voorkomt, en dus handig gebruikt kan worden bij de beschrijving van het gehele patroon. De boven beschreven berekening van de ordeningsmaat, die gebruik maakt van de informatie-inhoud van een herkodering van het input-patroon in termen van supertekens, moet dus voorafgegaan worden door een andere berekening, die vaststelt welke supertekens er überhaupt gebruikt worden. Dit onderdeel van de berekening van de Esthetische Maat wordt in de informatie-esthetische literatuur niet gespecificeerd.

Leeuwenberg en de Prägnanz.

Er is een andere onderzoekstraditie die een centrale plaats toekent aan de context-afhankelijkheid van de constitutie van de supertekens. Dat is de psychologische traditie van de Gestalt-waarneming, in de twintiger jaren geïnitieerd door Max Wertheimer en Kurt Koffka. De Gestaltpsychologen benadrukken dat de door een input-patroon opgeroepen totaal-indruk (de "Gestalt") op een zeer complexe wijze door dat input-patroon bepaald wordt. Er spelen daar allerlei, mogelijkerwijs konflikterende, faktoren een rol. Een van de belangrijkste faktoren, die de doorslag geeft in situaties die in principe meerdere mogelijkheden zouden toelaten, is de voorkeur voor de eenvoudigste struktuur. Deze faktor wordt wel het Principe van de Prägnanz genoemd.

De oorspronkelijke Gestaltwaarnemingstheorie van Wertheimer en Koffka was nog geen mathematisch geformuleerd model. Die stap wordt pas aan het eind van de zestiger jaren gezet, door de Nijmeegse psycholoog Emmanuel Leeuwenberg. Net als de informatie-esthetici beschrijft hij de waarneming als een her-coderings-proces. De "ruwe input" wordt beschreven als een eenvoudige opsomming van elementaire constituenten. De perceptieve "Gestalt" die deze input oproept in de geest van de beschouwer, wordt gemodelleerd als een compactere codering van hetzelfde beeld -- een codering waarin de waargenomen struktuur van het patroon expliciet teruggevonden kan worden.

De informatie-esthetica heeft ons al een eerste indruk gegeven van hoe zo'n her-codering er dan uit zou kunnen zien. Een informatie-esthetische her-codering van een rasterbeeld vermeldt hoe het vlak is gevuld met supertekens; voor elk superteken is dan weer aangegeven hoe het opgebouwd is uit kleinere supertekens; en zo verder, tot het niveau van de elementaire tekens bereikt is. De recursieve constituenten-struktuur van het beeld is daarmee expliciet gerepresenteerd. Maar de informatie-esthetische analyse van de her-codering is beperkt in verschillende opzichten: het gaat alleen om rasterbeelden; de informativiteitsberekening van deze coderingen gaat ervan uit dat supertekens alleen gekonstrueerd kunnen worden door het naast elkaar plaatsen van kleinere supertekens die onafhankelijk van elkaar gespecificeerd zijn; en supertekens niet expliciet gerepresenteerd kunnen worden als varianten of transformaties van elkaar. Hoewel begrippen als "herhaling", "spiegeling", "rotatie", etc. onderdeel vormen van de Gestalt die iemand vormt van een input-patroon, kunnen we die niet aanwijzen in de informatie-esthetische her-codering van zo'n patroon .

Leeuwenberg stelt daarom een veel rijkere beeldcoderingstaal voor, met operatoren die elk visueel patroon tot allerlei andere patronen kunnen transformeren, door het te vergroten, te verkleinen, te roteren, te spiegelen, etc., of op diverse wijzen te kombineren met andere patronen; en met operatoren die uit elk visueel patroon een complexer patroon kunnen opbouwen, door het (al of niet getransformeerd) te herhalen, of met andere patronen te alterneren. Als paradigmatisch beeld-genre gebruikt Leeuwenberg niet symbool-rasters, maar tekeningen die opgebouwd zijn uit rechte lijnstukjes. De expressies van zijn codeertaal lijken daardoor sterk op sequenties van plotter-besturings-opdrachten, zoals b.v. in de turtle-graphics van het LOGO-systeem. De codering van de ruwe input bestaat uitsluitend uit opdrachten van de soort: zoveel stappen vooruit; zoveel graden naar links; . . . Maar bij de her-codering worden dan bovendien "hoog niveau" operaties gebruikt, die een reeds gedefinieerde figuur dupliceren, verschuiven, roteren, etc.

Hiermee stelt Leeuwenberg op de eerste plaats een hypothese aan de orde over de formalisering van de Gestalt-waarneming: het idee dat je in zo'n turtle-graphics-taal zinnige representaties van Gestalt-percepten kan uitdrukken. Uitgaande van de correctheid van deze hypothese, probeert hij dan om de Gestalt-waarnemings-verschijnselen binnen zijn model te beschrijven. Dat gebeurt dan door Gestalt-waarneming te modelleren als een disambigueringsproces. De codering van de ruwe input laat altijd een groot aantal alternatieve her-coderingen toe, en de vraag is dan: welke is de her-codering die het menselijk brein in feite genereert?

Om die vraag te kunnen beantwoorden vereenzelvigt Leeuwenberg de psychologische complexiteit van een Gestalt met de lengte van de turtle-graphics-code die ermee overeenkomt -- waarbij die lengte gemeten wordt door het aantal voorkomens van visuele basis-elementen in die code te tellen. Het Prägnanz-principe is daarmee geformaliseerd: de geprefereerde her-codering van een input-patroon is eenvoudigweg de kortste her-codering, en de waargenomen Gestalt is de Gestalt die daarmee overeenkomt. In figuur 4 bijvoorbeeld, zien we van twee simpele patronen elk drie verschillende structurele interpretaties, a,b en c. Voor het eerste patroon geeft interpretatie c de kortste code. Voor het tweede patroon is dat interpretatie a.

Figuur 5: Twee lijntekeningen met elk drie verschillende analyses.
Bij A is c de perceptief geprefereerde analyse. Bij B is dat a. (Naar: H. Buffart)

Leeuwenberg's theorie is getest op zeer uiteenlopende visuele patronen, en ook op muzikale waarneming. In veel gevallen heeft dit tot bevredigende empirische resultaten geleid.

Leeuwenberg's benadering suggereert een interessante variant van de informatie-esthetische ordelijkheidsmaat. Een patroon dat uit herhalingen van hetzelfde element bestaat, wordt als ordelijker ervaren dan een patroon met allemaal verschillende elementen. De informatie-inhoud van een Leeuwenberg-codering, waarin dat verschil expliciet zichtbaar is, levert daarom een betere ordelijkheidsmaat dan het oorspronkelijke informatie-esthetische voorstel, dat de informatie-eenhoud van alle individuele beeld-elementen optelde. Een bijkomend voordeel is, dat we met een Leeuwenberg-codering niet vastzitten aan zo beperkte genres als rasterpatronen.

Waarneming en ervaring.

Maar niet alle onderdelen die we in een beeld onderscheiden zijn herhalingspatronen of elementen in herhalingspatronen. Wie bijvoorbeeld een figuratief schilderij aanschouwt, zal getroffen worden door gelijkenissen met eerder waargenomen objekten en situaties. Als we dit verschijnsel willen meenemen in de berekening van de informatie-inhoud van de minimale Leeuwenberg-code van een input-patroon, dan kunnen de primitieven van de waarnemingstheorie niet beperkt blijven tot pixels of simpele lijnstukjes. We moeten dan een van de ideeën van de informatie-esthetiek opnieuw introduceren: een tevoren bepaald repertoire van "supertekens", dat bij de her-codering van een input-beeld gebruikt wordt.

Hoe moeten we dat supertekenrepertoire dan specificeren? In de contekst van een Leeuwenberg-achtige benadering is dat duidelijker dan bij de oorspronkelijke informatie-esthetiek. Ons vermogen om regelmatige abstrakte patronen te herkennen wordt al verantwoord door de strukturele eigenschappen van de coderingstaal. De supertekens zijn alleen nog nodig om de rol van de ervaring in rekening te brengen. Dat kunnen we doen door alle tekencomplexen die als betekenisvolle constituenten in eerdere ervaringen voorkwamen als supertekens te erkennen. Maar niet allemaal in dezelfde mate, want een superteken wordt gemakkelijker herkend naarmate het vaker voorgekomen is. Volgens Shannon is de informatie-inhoud van een superteken de logaritme van de a priori kans dat het superteken optreedt. Iemand kan die kans in eerste benadering schatten als de tot dusver ervaren voorkomensfrekwentie van dat superteken. Deze berekening kan verder verfijnd worden door te werken met conditionele kansen, die de onderlinge afhankelijkheid tussen de analyses van de verschillende onderdelen van het beeld in rekening brengen.

Voor het geval van taalwaarneming is deze benadering al in enig detail uitgewerkt. De geprefereerde analyse van een taaluiting is die analyse die het vaakst gegenereerd wordt door het willekeurig met elkaar kombineren van willekeurige deelbomen uit een corpus met eerder waargenomen taaldata. Dit komt overeen met een voorkeur voor de kortste code: voor analyses die opgebouwd kunnen worden uit zo weinig mogelijk zo waarschijnlijk mogelijke brokstukken.

Naar een proces-model.

Terugblikkend op deze beknopte geschiedenis van de computationele esthetica, zien we enige vooruitgang, maar ook heel duidelijke beperkingen. De vooruitgang betreft het langzamerhand uitkristalliseren van een begrippenapparaat dat kan dienen om een aantal elementaire eigenschappen van het Gestaltwaarnemingsproces formeel te beschrijven. De beperkingen betreffen vooral de schoonheidsopvatting die hier vormgegeven wordt. We hebben al opgemerkt dat Birkhoff's "Esthetische Maat" beter "ordelijkheidscoëfficiënt" genoemd had kunnen worden, en dat hetzelfde geldt voor de informatietheoretische verfijning ervan die we op basis van Bense's en Leeuwenberg's ideeën gesuggereerd hebben. Aan al deze modellen ligt een opvatting ten grondslag die de schoonheidservaring vereenzelvigt met het waarnemen van formele regelmatigheden die vervat liggen in het beschouwde objekt -- en ze laten dan ook nog de intensiteit van de schoonheids-ervaring rechtstreeks afhangen van de hoeveelheid regelmatigheden.

Als we terugdenken aan Kant's definitie van de schoonheidservaring als het bewustzijn van het vrije spel van de cognitieve vermogens, dan is het duidelijk dat deze opvatting te statisch is; dat een adekwater model betrekking zou moeten hebben op de aard van de waarnemingsprocessen, en niet alleen op het eindresultaat. In zo'n proces-model zouden we dan ook kunnen proberen om een aspekt van het esthetische mee te nemen dat in de tot dusver besproken harmonie-modellen geen plaats kon vinden: de belangrijke rol die gespeeld wordt door ongedefinieerdheid en ambiguïteit, zowel op het niveau van de Gestalt-waarneming als op het niveau van de interpretatie.

Enkele aanzetten voor zo'n proces-model kunnen we wel vinden in het hierboven besprokene. De codeertheorie die we voorgesteld hebben zou niet alleen moeten voorspellen tot welke Gestalt een bepaalde input aanleiding geeft, maar ook, welke inputs aanleiding geven tot een aantal verschillende Gestalten die een onderling vergelijkbare plausibiliteit hebben, zodat ze als ambigu ervaren worden. En bovendien, in welke gevallen die verschillende Gestalten ook weer interessante relaties met elkaar onderhouden, zodat ze niet met elkaar concurreren, maar leiden tot associatieve cycli -- tot superGestalten, tot processen die lijken op een definiete waarneming maar die een veel rijker karakter hebben, omdat ze een groot aantal verschillende (en mogelijkerwijs incompatibele) waarnemingen in één coherent geheel omvatten. Onze hypothese is, dat de schoonheidservaring gekenmerkt wordt door dit soort processen, die in zekere zin de waarneming voor zichzelf toegankelijk maken, omdat er een waarnemingsproces aan de hand is waarin tussenresultaten en alternatieve hypothesen stabiel genoeg zijn om tot het bewustzijn door te dringen -- iets wat normalerwijs gedurende de doelgerichte waarneming van duidelijke input niet mogelijk is.

Zo'n proces-model zou voor een overzichtelijke klasse van inputs (lijntekeningen of rasterpatronen, bijvoorbeeld) wel uit te werken zijn. Maar er is absoluut nog geen sprake van om zoiets te doen terwijl we alle mogelijkheden van de menselijke visuele waarneming simuleren. Nog moeilijker wordt het als we de semantische dimensie erin betrekken -- als we er rekening mee houden dat de schoonheids-ervaring niet alleen een kwestie is van Gestalt-waarneming, maar evenzeer van betekenis-toekenning. Op dat gebied is het niet mogelijk om serieuze simulaties te doen. Wel kunnen we spekuleren over hoe het struktureel in elkaar zou moeten zitten.

Het is duidelijk dat we dan niet alleen de letterlijke betekenissen van konventionele tekens en herkenbare afbeeldingen moeten beschouwen, maar ook de betekenissen die worden opgeroepen door middel van metaforische of metonymische projektie van de waargenomen strukturen op het ervaringsmateriaal van de beschouwer. Opnieuw gaat het er dan om, dat er niet te snel definiete interpretaties ontstaan, maar eerder complexen van onderling gerelateerde alternatieven. Zoals Roland Barthes in  Éléments de Sémiologie al aangaf, moet vervolgens het hele systeem recursief worden toegepast: de eerste betekenissen kunnen (in de context van de andere geobserveerde strukturen en betekenissen) doorgeïnterpreteerd worden tot "diepere" betekenissen, en zo verder.

Zo'n semantisch georiënteerd model is voorlopig niet in enig detail uit te werken. Toch kan het een zekere konkrete voorstelbaarheid krijgen, zeker zodra een heel beperkt zuiver syntaktisch model interessante resultaten zou laten zien. Aldus zal uiteindelijk de grootste winst van de computationele modellering van het esthetische niet liggen in de modellen die implementeerbaar en valideerbaar zijn -- maar in de meer spekulatieve en veelomvattende modellen die daardoor denkbaar gemaakt worden.

Literatuur.

Roland Barthes:  Éléments de Sémiologie. Paris: Éditions du Seuil, 1964.

Max Bense: Aesthetica. Einführung in die neue Aesthetik. Baden-Baden: Agis-Verlag, 1965.

G.D. Birkhoff: Collected Mathematical Papers, New York: American Mathematical Society, 1950.

Rens Bod: "Using an Annotated Corpus as a Virtual Grammar." Proceedings EACL'93, Utrecht, 1993.

William Desmond: Art and the Absolute. Albany, NY: SUNY Press, 1986.

Karl Gerstner: "The Precision of Sensation" In: H. Stierlin (red.): "The Spirit of Colors. The Art of Karl Gerstner". Cambridge, Mass.: The MIT Press, 1981.

R. Gunzenhäuser: Mass und Information als ästhetische Kategorien. Baden-Baden: Agis Verlag, 1975.

Immanuel Kant: Kritik der Urteilskraft. 1799.

Susanne Langer: Problems of Art. New York: Charles Scribner's Sons, 1957.

E.L.J. Leeuwenberg: "A Perceptual Coding Language for Visual and Auditory Patterns." Am. J. Psychology, 84 (1971).

Remko Scha: "Virtuele Grammatica's en Creatieve Algoritmen." Gramma/TTT, 1,1 (1992).

Claude E. Shannon: "A Mathematical Theory of Communication." Bell Syst. Techn. J., 27 (1948).