Computational Esthetics

Remko Scha and Rens Bod

Formal theories which compute the "beauty coefficient" of visual patterns, fail to do justice to the complexity of the esthetic experience. These "computational esthetic" models do, however, embody some notions that are needed to build formal models of human perceptual processes -- and these, in their turn, must be the basis of any empirically adequate esthetic theory.

Though the esthetic experience remains one of the most enigmatic side-effects of human perception, several mathematical models have been proposed which assign to visual patterns a "beauty coefficient" -- a number that is intended to correlate with the degree of esthetic pleasure the pattern evokes. Such theories seem a little naive, because they focus on a quantitative and absolute beauty judgment. They disregard the qualitative aspects of specific esthetic experiences, and do not account for the context-dependence and variability of beauty-judgments. It is interesting, nevertheless, to look at the operation of these excessively simplistic beauty calculations; if we integrate them with other ideas from perceptual psychology and computational linguistics, they may in fact constitute a starting point for the development of more adequate formal models.


Kant and the beauty experience.

The best analysis of the esthetic is still Immanuel Kant's. He viewed the experience of beauty as the consciousness of a psychological process: the pleasing awareness of the harmony in the free play of our cognitive faculties. If Kant is right about this, the natural phenomenon or art object that thrills us is in fact not much more than a trigger. Then we must, to understand the esthetic, first of all understand the perceptual processes; apparently these are such that, helped by the properties of their input, they can bootstrap themselves into esthetic experiences.

Kant's analysis implies that the objectivity of esthetic judgments is not self-evident. He construed it as an intersubjectivity -- as an indirect consequence of the high degree of similarity between the cognitive machineries of different persons. He nevertheless disputed the validity of completely arbitrary individual esthetic judgments by positing the "better developed" taste as the norm. Later philosophers have often pointed out that this is one of the weaker spots in Kant's story. A psychological notion of beauty is necessarily subjective, and certainly not normative.

Against this background, a notion of beauty that only classifies objects as beautiful, less beautiful, neutral, or ugly, must be viewed as naive. Nevertheless it is such a notion that underlies all formal theories of beauty proposed so far. Perhaps we shouldn't be surprised about this. Many much more commonplace aspects of perception have not yet been formally analyzed either; it is therefore not realistic to expect today's mathematical theories to face all complexities of the esthetic.

That existing formal theories only account for caricatures of the beautiful, is thus not a sufficient reason to dismiss them altogether. It would be sufficiently interesting if they analyze certain aspects of the esthetic in a way that can be extended or refined. From that perspective, this article looks at some of these theories, and then reconsiders what would be involved in a more adequate computational model of esthetic processes.

Birkhoff and harmony.

Twentieth-century formal theories of beauty tie in with earlier informal theories which focussed on the feeling of harmony in the experience of beauty, and which explained that feeling as arising from our resonance with the harmonious properties of the object that is being observed -- with self-similarities, symmetries, and simple proportions in the appearance of that object. In this view, beauty is in essence a mathematical phenomenon. The ancient Pythagoreans were not the only ones who explicitly held this opinion. G.W. Leibniz, for instance, described the enjoyment of art as the unconscious calculation of numerical proportions -- between time intervals, in the case of music, or between spatial distances, in the case of visual art and architecture.

In 1928, the American mathematician George David Birkhoff made the first attempts to formalize such notions. He introduced the concept of the Esthetic Measure (M), defined as the ratio between Order (O) and Complexity (C): M = O/C. The Complexity is roughly the number elements that the image consists of; the Order is a measure for the number of regularities found in the image. For different artistic genres, Birkhoff has indicated specific rules to actually compute precise values for Order and Complexity.

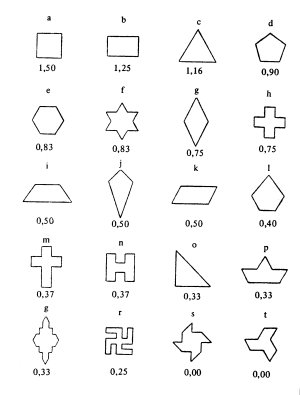
For polygons he thus defines Complexity as the number of edges, while the numerical value for Order depends among other things on the presence of vertical symmetry, point symmetry, and mechanical stability with respect to an imaginary horizontal plane. Figure 1 shows for some polygons the value for the Esthetic Measure that is computed in this way. As one might expect, the highest scores go to patterns with a minimal number of parts and a maximal number of symmetries. The square wins.

Figure 1:
The esthetic measure of some polygons
according to Birkhoff's formula: M = O/C.
(After: G.D. Birkhoff)

Birkhoff's formula thus turns out to formalize the idea of "orderliness" rather than the idea of "beauty". And to identify orderliness and beauty, though not impossible, seems to be a very specific esthetic choice. Artistic movements such as ZERO, NUL and minimal art actually made such a choice. In the constructivist tradition this idea also plays an important role: "If a picture works out without a remainder, that means that all its elements are logically related to each other; it means that each color corresponds to every other, each form to every other, each form to every color and both form and color to their contents. It means ultimately: that its structure is homogeneous, from conception to perception." (Gerstner, 1981, p.35.)

Birkhoff, however, was not making an artistic statement or propounding a normative theory; he viewed his model as an empirical theory, and was interested in its validity. He has therefore presented his polygons to students, and compared their beauty judgments with those of his formula. He never published the details about these experiments, but he was satisfied with their results ("the judgments of students seem to indicate the validity of the formula"). More recent psychological experiments, however, only yielded a weak correlation between Birkhoff's measure and the actual beauty judgments of the subjects. This context-dependence of the esthetic judgments is not surprising: there is no reason to suppose that people entertain one fixed notion of beauty, which can be activated with an arbitrary laboratory-experiment. It is much more plausible that there are many different classification criteria, all in some way related to the esthetic dimension of perception, that people may apply in different situations.

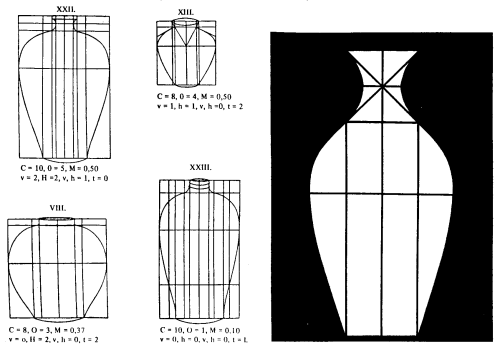
For a different domain, a class of Chinese vases, Birkhoff defined the numerical value for Order in a rather different way. His point of departure is the two-dimensional projection of the vase. He then draws tangents, horizontal lines and vertical lines through the points of maximal, minimal and zero curvature on the outline of the vase; and he counts how many intersections of such lines coincide with each other, and how many pairs of intersection points are equidistant. Figure 2 illustrates how Birkhoff arrives at the vase with the highest Esthetic Measure.

Figure 2.
Left: the esthetic measure of some vase shapes according to Birkhoff's formula: M=O/C.
Right: the 'ideal vase' according to Birkhoff. (After: G.D. Birkhoff)

The formula behaves in a more interesting way now. The Esthetic Measure now correlates with a quality of "elegance", rather than a trivial property of orderedness. The reason is, that the objects which are to be compared are now defined in a different (more limited) way: all the different vase shapes are distortions of one basic shape. The shapes can thus be compared more accurately with each other, in terms of the quantity of additional internal coherence they display. Once more we find, in this way, the singularities within a space of possibilities -- but now they are less predictable.

The exemplars classified as "beautiful" now indeed have something of the "organic unity" that is often viewed as a characteristic of the succesful artwork: "Every element in a work of art is so involved with other elements in the making of the virtual object, the work, that when it is altered (as it may be -- artists make many alterations after the composition is well under way) one almost always has to follow up the alteration in several directions, or simply sacrifice some desired effects. [...] This many-sided involvement of every element with the total fabric of the poem is what gives it a semblance of organic structure; like living substance, a work of art is inviolable; break its elements apart, and they no longer are what they were -- the whole image is gone." (Langer, 1957, pp. 55-57.)

Birkhoff has also worked out specific versions of his formula for the auditory dimension of poetry, and for melodies. We will not discuss these in detail; the above suggests that it is by no means obvious what they should look like, and what kind of intuition of beauty would be formalized then. This betrays a weak point in Birkhoff's "theory": for every genre of input objects, new rules must be formulated, and the notion of beauty embodied by Birkhoff's formula may therefore shift a little in each case.

Bense and Information Theory.

It is not surprising, therefore, that some researchers have tried to use Birkhoff's idea as a point of departure for developing a more general, encompassing theory.The most important case in point is a group of literary theorists in Germany in the fifties, headed by Max Bense. This group has developed the theory of information esthetics -- a Birkhoff-like model of beauty judgments, formulated in terms of Claude Shannon's information theory.

The starting point is Birkhoff's original formula: M = O/C. The definition of the Complexity of an input pattern is then borrowed from Shannon's notion of Information: if an input pattern specifies n binary choices from the class of possible patterns, the Complexity equals n.To be able to compute the Complexity in a direct way, one introduces the assumption that an input pattern can always be described as a two-dimensional grid of discrete symbols from a pre-defined repertoire. If the repertoire contains k symbols which all have an equal a priori chance of occurring, every symbol has an information content which correponds to 2log k binary choices. The information content H1 of an m by n grid is then n * m * 2log k, and that is the value assigned to the Complexity C of such a pattern.

Figure 3: Some grid patterns in order of increasing orderliness: increasingly large 'supersymbols'. (After: Gunzenhäuser, 1975)

To arrive at a similar information-theoretic articulation of Birkhoff's notion of Order, we observe that orderliness corresponds to the possibility of perceiving larger structures. If these larger structures can in their turn be considered as discrete "supersymbols" within a well-defined repertoire, we can compute the information-content H2 of the pattern as described in terms of these supersymbols. If not all combinations of elementary symbols are considered as legitimate distinct supersymbols, the new coding is more parsimonious than the original one, so H2 is smaller than H1: the description in terms of supersymbols yields an "Ordnungsgewinn". The degree of orderliness of the pattern corresponds to the difference between the information-content of the original coding and the information-content of the supersymbol-coding: H1 - H2. Birkhoff's Esthetic Measure is thus computed as: M = (H1 - H2)/H1.

Bense's idea thus stays rather close to Birkhoff's original intuition, but nevertheless suggests a somewhat different model of the perceptual process. For Birkhoff, the experience of orderliness is a direct consequence of the perception of a relatively large number of regularities; in information esthetics, the experience of orderliness is a result of the transition between an initial coding of the input (in terms of individual line segments, words or tones) and its more parsimonious recoding which comes about after some reflection.

The information-esthetic formula therefore corresponds to well-known ideas about the role of the artwork's perceptual unity in the experience of beauty: "Initially, the details of the work seem to be just there, and we may seem free to conjoin them this way or that, whichever way we please. Yet if we dwell with the art work, and if this work is genuine, it comes to crystallize into a whole: the parts fit together and we discern a certain necessity in their cohesion. And since we are now guided by this sense of necessity, we are forced to discard our "old" freedom. But we do not experience this necessity as a mere external constraint. Rather it comes to us as a liberation, a release: we are freed from the fragmentariness of mere detail and come to be at home in a rich whole. It is not that we discard or obliterate the details, but in standing beyond their fragmentariness we ourselves are freed from fragmentation. Such a "standing beyond" which unites and preserves the internal details of a complex whole, in fact, makes the art work an aesthetic concretion of Hegel's general principle of Aufhebung". (Desmond, 1986, p. 64.)

Bense's information esthetics is, however, not more general than Birkhoff's theory. It is better viewed as an addition to Birkhoff's list of rules for specific genres. Information esthetics gives rules for computing Complexity and Order for a very specific kind of image: a grid consisting of discrete symbols from an explicitly specified finite repertoire. There is suggestion of generality, because in a technical sense all images may be viewed that way, at least approximately, if we think of them as built up out of pixels. But the suggestion is false, because for most images encountered in practice, a construction out of adjacent discrete elements is not the perceptually relevant analysis.

Information esthetics also inherits Birkhoff's preference for minimalist structures. The simpler the image, the more compact its supersymbol-coding can be, and the larger the resulting "Ordnungsgewinn". But exactly in the case of grid patterns it is clear that the preference for "total order" leads to incorrect results. It has often been remarked that an intuitive measure of beauty should not only get a null value when a pattern is too complex to to observe any order in it (random patterns: figure 4, upper left), but also when a pattern is ordered completely into perfect banality (figure 4, lower right). Complete disorder and complete order are perceptually approximately identical. The maximal value of the Esthetic measure should be found somewhere between these two poles.

Figure 4: Some grid patterns in order of increasing orderliness. (After: Gunzenhäuser, 1975)

There is another problem with the information-esthetic measure: the computation is based on a pre-defined repertoire of supersymbols. But many forms of orderliness, and not the ugliest ones, employ supersymbols defined by the artwork itself. A particular combination of elementary symbols can function as a supersymbol, merely because it (or a pattern derived from it) occurs more often in the total pattern, and can thus be employed conveniently for describing the whole pattern. To compute an orderliness measure on the basis of a recoding of the input pattern in terms of supersymbols, one must first compute which supersymbols are being used in the first place. This component of the computation of the Esthetic Measure is not specified in the information-esthetic literature.

Leeuwenberg and Prägnanz.

The context-dependence of the supersymbols was appreciated already by the psychological tradition of Gestalt perception, initiated in the twenties by Max Wertheimer and Kurt Koffka. The Gestalt psychologists emphasize that the overall impression (the "Gestalt") evoked by an input pattern, is determined by that input pattern in a very complex way. Various possibly conflicting factors play a role. One of the most important ones, which settles the outcome in situations which in principle would allow several possibilities, is the preference for the simplest structure. This factor is sometimes called the principle of Prägnanz.

The original Gestalt perception theory as developed by Wertheimer and Koffka was not yet a mathematically formulated model. That step was made in the late sixties by the psychologist Emmanuel Leeuwenberg in Nijmegen. Like the information-estheticians, he describes perception as a recoding-process. The "raw input" is described as a simple enumeration of occurrences of elementary constituents. The perceptual "Gestalt" which this input evokes in the mind of the observer, is modelled as a more compact coding of the same image -- a coding which explicitly represents the perceived structure of the pattern.

Information esthetics has given us a first impression of such a recoding. An information-esthetic recoding of a grid pattern indicates how the plane is filled by supersymbols; and for each of these supersymbols it indicates how it is built up out of smaller supersymbols; and so on, until the level of elementary symbols has been reached. The recursive constituent structure of the image is thus represented in an explicit way. The information-esthetic recoding process is limited in several respects, however: it only deals with grid patterns; it assumes that supersymbols can only be constructed by putting smaller, independently defined supersymbols next to each other; and supersymbols cannot be explicitly represented as variants or transformations of each other. Though notions such as "repetition", "mirror-image", "rotation", etc. play a role in the perceived Gestalt of an input pattern, they do not occur in the information-esthetic recoding of such a pattern.

Leeuwenberg therefore proposes a much richer image-coding language, with operators which can transform any visual pattern into various other patterns by rescaling or rotating it, or by repeating it or alternating it with other patterns. Leeuwenberg's paradigmatic images are not symbol grids, but drawings built up out of straight line-segments. The expressions of his coding language thus resemble sequences of plotter-control commands, as in the turtle graphics of the LOGO system. The coding of raw input consists exclusively of commands of this sort: so many steps ahead; so many degrees to the left; . . . But in recoding the analysed input, high level operations are also used, which duplicate , move, or rotate a figure that was defined before.

Leeuwenberg thus broaches a hypthesis about the formalisation of Gestalt-perception: the idea that such a turtle-graphics language can express meaningful representations of Gestalts. Assuming the correctness of this hypothesis, he then attempts to describe Gestalt-perception phenomena within his model, by modelling Gestalt perception as a disambiguation process. The coding of the raw input always allows a large number of alternative recodings, and the question is: which is the recoding actually generated by the human brain?

To answer that question, Leeuwenberg identifies the psychological complexity of a Gestalt with the length of the corresponding turtle-graphics code, as measured by counting the number of occurrences of basic visual elements in that code. This formalizes the Prägnanz-principle: the preferred recoding of an input pattern is simply the shortes recoding, and the perceived Gestalt is the gestalt corresponding to that recoding. In Figure 4, for instance, we see three different structural interpretations (a, b and c) of two simple patterns. For the first pattern, interpretation c yields the shortest code. For the second pattern, the shortest code corresponds to interpretation a.

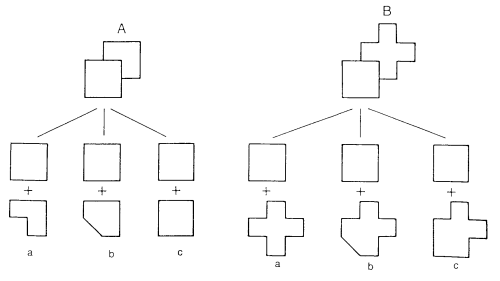
Figure 5: Two line drawings with three different analyses each.
For A, the perceptually preferred analysis is c. For B, this is a. (After H. Buffart)

Leeuwenberg's theory was tested on different kinds of visual patterns, and on musical perception. In many cases this yielded satisfying empirical results.

Leeuwenberg's approach suggests an interesting formulation of the information-esthetic orderliness-measure. A pattern consisting of repetitions of the same element, is experienced as more orderly than a pattern of elements which are all different. The information-content of a Leeuwenberg-code, which directly correlates with that distinction, thus results in a better orderliness-measure than the original information-esthetic proposal, which involved adding up the information-content of all individual image-elements. An additional advantage is that the applicability of Leeuwenberg's approach is not limited to specific genres such as grid patterns.

Perception and experience.

Not all parts that we distinguish in an image are repetitive patterns or elements in repetitive patterns, however. The observer of a figurative painting, for instance, will be struck by resemblances with previously perceived objects and situations. If we want to take this phenomenon into account in the computation of the information-content of the minimal Leeuwenberg-code of an input-pattern, the primitive elements of perception theory cannot be restricted to pixels or simple line segments. We must re-introduce one of the ideas of information-esthetics: a pre-determined repertoire of "supersigns", to be used in re-coding an input-image.

How is this supersign repertoire to be specified? In the context of Leeuwenberg's approach this is easier to decide than in the original information-esthetic framework. Our capacity for recognizing regular abstract patterns is already accounted for by the structural properties of the coding language. The supersigns are only needed to put the role of experience into the picture. To do that, all sign complexes which occurred as meaningful constituents in previous experiences should be recognized as supersigns. But not all to the same extent, because a supersign is recognized more easily the more often it has occurred. According to Shannon's wellknown formula, the information content of a supersign is the logarithm of the a priori probability of its occurrence. This probability can be estimated as the observed relative occurrence frequency of the supersign. The calculation can be further refined by working with conditional probabilities, which reflect the mutual dependencies between the analyses of the different parts of the image.

For the case of language perception, we have already worked out this approach in some detail. The preferred analysis of a language utterance is the analysis which results most often from the process of randomly combining random subtrees from a corpus with previously experienced language data. This corresponds to the preference for the shortest code: the preference for analyses which can be built up from a maximally small number of maximally probable fragments.

Towards a process model.

Looking back at this short history of computational esthetics, we see some progress, but we also notice obvious limitations. In particular, we see the gradual development of a conceptual framework which may make it possible to describe some elementary properties of the Gestalt perception process in a formal way. But the notion of "beauty" that is being articulated here, is extremely narrow. We mentioned already that Birkhoff's "Esthetic Measure" is in fact merely an "orderliness-coefficient", and this characterization also applies to the the information-theoretic versions of this notion based on Bense or Leeuwenberg. All these models identify the experience of beauty with the perception of formal regularities in the object that is observed, and they correlate the intensity of the experience directly with the number of regularities.

From a Kantian perspective which analyzes the esthetic experience as the awareness of the free play of the cognitive faculties, these models are too static; a more adequate model should be concerned with the nature of the perceptual processes rather than their end result. Such a process model might also account for the important role that undefinedness and ambiguity play in the esthetic experience, both at the level of Gestalt perception and at the level of interpretation. Though the orderliness-models as they stand completely ignore this aspect of the esthetic, they might nevertheless provide a starting point for the design of a more adequate process-model.

The coding theory that we proposed should not only predict the Gestalt that a particular input evokes, but also, what inputs are experienced as ambiguous because they evoke several distinct Gestalts that are roughly equally plausible. And they should predict in which cases these distinct Gestalts are mutually related in such a way that they do not compete with each other, but give rise to associative cycles — superGestalts, i.e., processes which resemble definite perceptions but which are much richer since they embrace a large number of different (possibly incompatible) perceptions in one coherent whole. We conjecture that the experience of beauty is characterized by processes of this sort, which allow perception to gain access to itself, because its intermediate results and alternative interpretive hypotheses are stable enough to reach consciousness — something which is impossible during the normal goal-directed perception of clear-cut input.

For a specific, narrowly defined class of inputs (such as line drawings or grids), such a process-model might be worked out. But it would be absolutely out of the question to accomplish this in the context of a complete simulation of all possibilities of human visual perception. Things get even more difficult when we introduce the semantic dimension — when we acknowledge that the experience of beauty involves not only the perception of Gestalts, but also the assignment of meanings. It is not possible to build serious simulations which involve the semantic realm. But it is possible, of course, to speculate about the structure that such simulations would have.

It is clear that they would not only involve the literal meanings of conventional signs and recognizable images, but also the meanings which are evoked when the structures perceived are mapped onto the observer's experiential background through metaphorical or metonymical projection. Again it is crucial that the interpretive processes do not yield definite interpretations too quickly, but rather give rise to complexes of mutually related alternatives. As Roland Barthes indicated in  Éléments de Sémiologie, this machinery is applied recursively: in the context of the other structures and meanings observed, the first layer of meanings can be re-interpreted to yield "deeper" meanings, and so on.

For the time being, we cannot work out such a semantic model in any detail. But it will become more concretely imaginable as soon as a very limited purely syntactic model would show interesting results. Thus, the ultimate benefit of the computational approach to the esthetic will not lie in the models that can be implemented and validated — but in the more speculative and encompassing models which they make thinkable.

Literature.

Roland Barthes:  Éléments de Sémiologie. Paris: Éditions du Seuil, 1964.

Max Bense: Aesthetica. Einführung in die neue Aesthetik. Baden-Baden: Agis-Verlag, 1965.

G.D. Birkhoff: Collected Mathematical Papers. New York: American Mathematical Society, 1950.

Rens Bod: "Using an Annotated Corpus as a Virtual Grammar." Proceedings EACL'93, Utrecht, 1993.

William Desmond: Art and the Absolute. Albany, NY: SUNY Press, 1986.

Karl Gerstner: "The Precision of Sensation" In: H. Stierlin (ed.): "The Spirit of Colors. The Art of Karl Gerstner". Cambridge, Mass.: The MIT Press, 1981.

R. Gunzenhäuser: Mass und Information als ästhetische Kategorien. Baden-Baden: Agis Verlag, 1975.

Immanuel Kant: Kritik der Urteilskraft. 1799.

Susanne Langer: Problems of Art. New York: Charles Scribner's Sons, 1957.

E.L.J. Leeuwenberg: "A Perceptual Coding Language for Visual and Auditory Patterns." Am. J. Psychology, 84 (1971).

Remko Scha: "Virtual Grammars en Creative Algorithms." Gramma/TTT, 1,1 (1992).

Claude E. Shannon: "A Mathematical Theory of Communication." Bell Syst. Techn. J., 27 (1948).